Untitled Scanned 26

- 52 -

y -    ♦. x₂ + x₃ • x₄ = _X1 + x₂ + x₃ • x₄ =

- *! + *₂ ^{+ x}3 ⁺ *4 ^{e X}1 ^{+ x}2 ^{+ x}3 ^{+ x}4

(schemat układu - rys.2.19d), a w przypadku wykorzystania elementów NAND

---■ ■■-■- i    _ - -

y - ^X1 + ^x2 ^{+ x}3 • ^x4 = ^X1 ^{+ x}2 ⁺-i^x3 • ^x4 ^{c x}r^x2‘^x3'^x4 (schemat układu - rys.2.20).

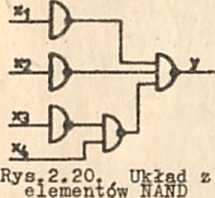
Realizacja układu na podstawie postaci normalnej nie zawsze prowadzi do rozwiązań o najmniejszej liczbie elementów NOR albo NAND. Jeżeli minimalna liczba elementów Jest sprawą łardzo ważną, korzysta się ze specjalnych metod minimalizacji.

2.6. STANY PRZEJŚCIOWE W UKŁADACH KOMBINACYJNYCH;

HAZARD

Opis działania układów kombinacyjnych w postaci równań logicznych dotyczy jedynie stanów ustalonych. Przy projektowaniu układów logicznych należy zdać sobie sprawę z tego, czy zjawiska występujące podczas trwania stanów przejściowych nie umożliwią wykorzystania układu zgodnie z jego przeznaczeniem.

Na przebieg procesów przejściowych w układzie kombinacyjnym mają wpływ następujące czynniki:

-    nieskokowy charakter zmian wartości sygnałów występujących w układach rzeczywistych,

-    opóźnienia wnoszone przez linie sygnałowe przy przesyłaniu przez nie sygnałów,

-    opóźnienia wnoszone przez elementy przy przetwarzaniu sygnałów.

Nieskokowy charakter zmian wartości sygnałów powoduje, że w stanach przejściowych sygnały przyjmują wartości nie będące ani stanem O, ani stanem 1. Czasy trwania stanów przejściowych (czas narastania i czas opadania) decydują o maksymalnej częstotliwości zmian sygnałów przetwarzanych przez układ.

Opóźnienia wnoszone przez linie sygnałowe i elementy danego układu mogą być przyczyną nieprawidłowego działania tego układu w stanach przejściowych.

W układach kombinacyjnych wyróżnić można dwa rodzaje stanów przejściowych:

-    stany, w których zmiana jednego z sygnałów wejściowych nie powinna, zgodnie z równaniem opisującym działanie układu, wywołać żadnej zmiany na wyjściu,

-    stany, w których zmiana jednego z sygnałów wejściowych,zgodnie z równaniem opisującym działanie układu, wywołuje zmianę wartości sygnału wyjściowego.

Zjawisko polegające na wystąpieniu krótkotrwałych zmian wartości sygnału wyjściowego, w czasie trwania stanów przejściowych pierwszego rodzaju, nazywa się hazardem etatycznym. Zjawisko polegające na wystąpieniu dodatkowych zmian wartości sygnału wyjściowego w stanach przejściowych drugiego rodzaju, nazywa się hazardem dynamicznym.

Hazard statyczny, występujący w układzie zrealizowanym .przy wykorzystaniu alternatywnej postaci funkcji, nazywa się hazardem w jedynkach, gdyż objawia się jako chwilowy zanik sygnału jedynkowego. Hazard statyczny, występujący w układzie zrealizowanym przy wykorzystaniu postaci koniunkcyjnej nazywa się hazardem w zerach, gdyż objawia się jako krótkotrwały im-pulB w okresie, w którym na wyjściu układu powinien istnieć stale sygnał o wartości 0.

Jeżeli funkcja, na podstawie ktćrej zrealizowany jeat układ ma postać

y = a + b •    + c •

gdzie: x₄ - jeden z argumentów funkcji, a - suma iloczynów elementarnych, b, c - iloczyny elementarne, to w układzie wystąpi hazard statyczny w jedynkach podczas zmian sygnału gdy a=0, b=1, c=1. W sytuacji takiej składniki bx_Ł oraz cz^ winny, zgodnie z zapisem algebraicznym, przyjmować wartości wzajemnie przeciwne, niezależnie od wartości x^. Zatem, przy