HPIM5173

L_**

ewolwenta wydłużona    b) ewolwenta

N I ewolwenta zwyczajna    zwyczajna

V

8

ewolwenta skrócona Jt okręgi zasadnicze

K

RVS. 3.11. a) linie cwolwcntowc. b) ewolwenta powstała jako obwiednia rodziny prostych a zwią-

“ cos a

stronie prostej k co koło zasadnicze, a punkt M" po stronie przeciwnej. Linie te odgrywają pewną rolę w geometrii kół zębatych.

Ewolwentę zwyczajną, pokazaną na rys. 3.1 la, można otrzymać również w inny sposób. Pokazany jest on na rys. 3.1 Ib. Ewolwenta jest tu obwiednią rodziny linii a połączonej trwale w punkcie A z linią b toczącą się bez poślizgu po kole o średnicy d, która jest związana ze średnicą koła zasadniczego dy_; zależnością

cos a

(3.33)

gdzie a jest kątem, który tworzy prosta a z normalną do prostej b.

Ten sposób powstawania ewolwenty jest stosowany przy nacinaniu zębów metodą obwiedniową.

Poznamy teraz pewne właściwości i zdefiniujemy pewne wielkości charakteryzujące geometrię ewolwenty.

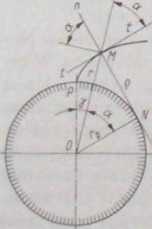
Na rysunku 3.12 pokazana jest ewolwenta okręgu zasadniczego, którego promień oznaczono przez rj,. Na ewolwencie zaznaczono dowolny punkt M leżący

ji

r=N0

<f=NM

RYS. 3.12.

Geometria ewolwenty

sadniczego jest równa odcinkowi MN, czyli

w odległości r od środka okręgu zasadniczego. W punkcie M prowadzimy linię n-n normalną do ewolwenty i linię t-t styczną do niej. Ze sposobu powstawania ewolwenty wynika, że normalna do ewolwenty jest styczna do okręgu zasadniczego. Punkt styczności oznaczono literą N. Odcinek p = NM jest promieniem krzywizny ewolwenty w punkcie M. Kąt a między normalną do ewolwenty a normalną do promienia r = MO jest kątem zarysu ewolwenty w punkcie M. (Kąt ten nazywany jest również kątem przypora.) Kąt zarysu występuje jeszcze w dwóch innych miejscach pokazanych na rys. 3.12. Szczególne znaczenie ma kąt zarysu a w punkcie M leżącym na okręgu podziałowym. Kąt ten nazywamy nominalnym kątem zarysu. Pokazany jest on również na rys. 3.7.

Ze sposobu powstawania ewolwenty wynika, że długość łuku PN okręgu za

PN= MN    (3.34)

Ponieważ

PN=r_b(y+a)    (3.35)

oraz

MN = r_b tga    (3.36)

to ze wzorów (3.34), (3.35) i (3.36) wynika, że

y = tg a - a    (3.37)

Kąt y jest więc funkcją kąta zarysu. Funkcja ta nazywa się inwolutą (skrót inv). Jej argumentem jest kąt zarysu a. Mamy więc

invęt = tga - a    (3.38)

Funkcja ta ma istotne znaczenie w obliczeniach geometrycznych kół zębatych. Przy korzystaniu ze wzoru (3.38) należy zwrócić uwagę, że od wartości tga odjąć należy kąt a wyrażony w radianach. Wartości funkcji inva są podane w tabl. 3.3.

Z rysunku 3.12 wynika, że promień krzywizny ewolwenty w punkcie M wyraża się wzorem

p = r*tga    _f | j '    .    (339)

O powszechnym zastosowaniu zarysów ewolwentowych zadecydowały następujące ich zalety:

-    zarysy ewolwentowe spełniają podstawowe prawo zazębienia, tzn. są zarysami sprzężonymi; cechę tę zachowują również przy zmianie odległości osi, co korzystnie wyróżnia je spośród innych zarysów sprzężonych;

-    zarysy ewolwentowe są łatwe do wykonania; obróbka kół zębatych o różnych liczbach zębów może być wykonywana tym samym narzędziem; dzięki możliwości zastosowania obróbek wykańczających (wiórkowanie, docieranie, szlifo-

249