MG!26

jak liczba wszystkich odchyleń ujemnych, ale również jednakowa jest liczba dodatnich i ujemnych odchyleń o określonej wielkości co do wartości bezwzględnej. Krzywa ma zatem maksimum przy x = p, dwa punkty przegięcia x = p ± o i po obu stronach symetrycznie zbliża się do osi odciętych. Prawdopodobieństwo, że wynik pomiaru x znajduje się w przedziale x_i<x<x₂, wyraża

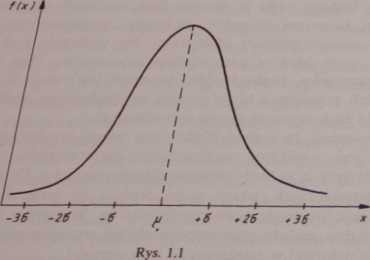
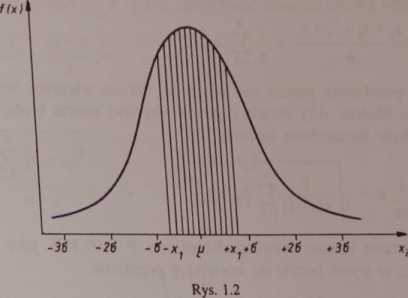
się graficznie polem odpowiedniego krzywoliniowego trapezu pod krzywą rozkładu prawdopodobieństwa. W szczególnym przypadku prawdopodobieństwo znalezienia się rzeczywistej wartości wielkości mierzonej w symetrycznym przedziale (-x_v, x_t), przy x_x > O, jest wyrażone polem figury zakreskowanej na rys. 12. Na podstawie tego rysunku można stwierdzić, że im mniejsza jest wartość o, tym mniejszy jest rozrzut błędów wokół p. Jeżeli błędy przypadkowe x podlegają rozkładowi normalnemu, to prawdopodobieństwo tego, że x przyjmie wartość z przedziału symetrycznego (-x_vx_l) oblicza się ze wzoru

(1.7)

(18)

P(-x, <x<xj = P(\x\<xJ « gdzie funkcja <&(t) nosi nazwę całki prawdopodobieństwa

/    _t*

*(t) = ~z=fe ⁷dt- lp(lxl<fo), t>0.

²

W pracy [13] są podane wartości funkcji 0(f). Prawdopodobieństwo, że błąd przypadkowy jest zawarty w dowolnym przedziale (x_vx^j dla rozkładu normalnego oblicza się ze wzoru

(1.9)

P(x,<x<xJ

Ostatecznie prawdopodobieństwo tego, że błąd przypadkowy przekroczy granice ±to (f > 0), jest równe

P(|x|>fo) = 1    (U-Ó)

Prawdopodobieństwo, że błąd pomiaru nie będzie większy od ± jednokrotnej, dwukrotnej, trzykrotnej itd., ogólnie f-krotnej wartości o, są podane w tablicy 1.1. Na przykład prawdopodobieństwo

P(|x| >3 o) = 1 ~2<D(t = 3) = 1 -0,9973 = 0,0027

jest tak małe, że wystąpienie błędu przypadkowego poza przedziałem trzysig-mowym jest praktycznie uważane za niemożliwe (prawo trzech sigm). Chociaż w rozpatrywanym modelu matematycznym dopuszcza się w zasadzie każdą wartość błędu, to jednak przyjmuje się, że wartości błędów przypadkowych pomiaru są ograniczone co do modułu wartością 3 o.

Tablica 1.1

Wartości prawdopodobieństwa

t	1 ^0	112		3	4
	1 ^0	0,6826 1	0,9346	0,9973	1,0000
	1 1	1 0,3174	0,0434	0,0027	1 I 1

Wartość średnia i odchylenie standardowe obliczane z próby są poprawne wtedy, gdy wyznacza się je z dużej próby, n z 30.

13