3582320539

Odwzorowania wieloliniowe Formy wieloliniowe Wyznaczniki

Przypomnienie:

N„ = {1,2,...,h}

Permutacją zbioru n-elementowego nazywamy każde bijektywne odwzorowanie tego zbioru na siebie

Przykład 0.

^={1,2,3,4,5},S = {3,2,5,1,4} a: A —>B

cri=cr(l) = ³

*, = °(2) = 2 _ltd.

Ilość permutacji = n!

§ - zbiór permutacji

W

Definicja 0.

Dwa elementy permutacji cr,cr tworzą inwersję jeżeli: <J_i><J_JAi< j Ilość inwersji w permutacji oznaczamyp= [<r], a znak permutacji określamy jako: e-(a) = (-l)^

Przykład 0'.

M = 5

®(°')=(-¹f^I=-¹

Jeżeli znak permutacji to +1 (parzysta ilość inwersji), to tę permutację nazywamy parzystą.

Jeżeli znak permutacji to -1 (nieparzysta ilość inwersji), to tę permutację nazywamy nieparzystą.

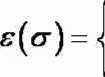
{a_va₂,...,a_n}

1    permutacja parzysta

_ l    permutacja nieparzysta

transpozycja - zamiana miejscami dwóch dowolnych elementów transpozycja zmienia znak permutacji

Wykład dr Magdaleny Sękowskiej strona 1 z 6 Częćć 9 - Odwzorowania wieloliniowa