3582323327

ZESTAW C

Zad.

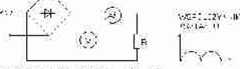
R=100£2, U=won IA=?

U=OtW2 Unj=U*V2 =565 Im=Unv' R=565/l00=5,65 Hx=2/ T f    [ni sinatdt=21ni/r f o*⁵ sincot tfc—

=2 Im/ T (-l/« cos(i)T/2)=2Im/ T{ -l/2itf *cos 2ltf*l/ S 2)=

^Im/ T*T/2^=£m/ Jt(cosjt - cosO)=2Im/ ję=3,6

Zad.

ZESTAW E

Zad

--i—-1 u(t)=2S2,San{314Ł-W3),P3tO(JW,I=10A₍R=?,C=?

P=U*t cosę U=282,8/V2=200Vcos9=400/200*10=0,2 9=78,4 9<j=60 9=91-91 91=60*78,4=18,4 U=aOOe>“MlOO+j 173,2    1=9, 4^3,1 Z=4,l+jI9,7

19,7=1/ 314C 0=1/314*1/19,7=161(1?

Zad.

I [=2QA, f=50Hz A1A2=? I=Wł/rfo^T i’{t)= Vl/Tfo^T Im’*sin^,<atdl= =V&n2/rfa^Tl/2(l-cos2ljX)<fc=Vlm2/2T f₀^T<ł>Im2/2T f₀^T cos2MdF =Vtoi2OT T=tm/v2 lm=C 72=20*1,41 =28,5A tWl/rfc™ Inp^cryald-W fm³ / T*1 /2{jó^Ta dt - fc^T’³ cos2o/tdt= =Vlm / 4=lm / 2    n =12=28,2/2=14,1 A

Zad

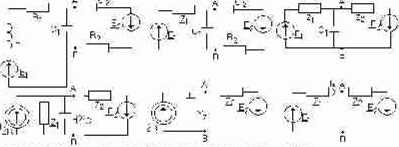
Zl=Rl+jXLl lix=£)JZl Y1=1/Z1 Y2=-l/jXc Y2=Y1+Y2    Z2=I/Y2    ®=Cs**Z2    Hr=i]+E2/Z1.+Z2

ZESTAW B

r-

•C|    -f.

R=Xc=10Jł, Uc=50V u(t}, i(t), p{lj=? Z=R^Xc U=C*Z U=l*(R-jXe) U=50+jJ0    9,*=0

[=Uc/-jXc=50/-jl0=36    i(t)=5V2sin(<at+»2)

Ujf=I*R=35*I0^j50V    9m=%/2    u(t.)=70V2 sń«UCHtf2)

p(t)=U*I cosę - U*I cos^utKpu+łpi)

Zad.

9=45-90= *45 Zad

	t- .	•^lr	,L
	'Hhl-im ■;			P
	iduV.^/iw			'•^<1 1. Ś*-P

U=Um/V2

■    R=201ł, t=2000T, f=50Hz

Um=4J*V2=400V Inf=Um/R=20A

r=i/l/Tfc^Tfl Im³*sin^,0]tA=VIm⁵/T*l/2{f₀^T'^,dt-f„^Ta <XK2Wdt=

=Vfai/4=Im/2 Itn=10A    T=I/F

Q=R*P*T=20*100*2000*l/50=80kJ

Zad.

U=220V, P=5kW,, f=5QHz, cosę=fl,7 9=46 91=0 P=U*I««9 1=5000' 220*0,7=32A Qc=Qc Qt,=O*Ianę=5064 Ic=Uc/Xc 5064=U*UZXc sinę 5064=tP/ Xc sin9=71ł 0J=2ltf=314 Xr=l/<oC C=l/Xc(d=I/7 *314=4,5*1 O* ZESTAW A

Zad

li=-46

l=E/2Rw=l 26/ 2*6=10,5A    1=11+12

E=126V, I2=6,26A, Rw=61ł, R1 i R2=?

a=C -12=10,5-6,26=4,24A    [M*Rw=10,5*6=63V

Uak=£1-U=126-63=63 Q =UWR1 ->Rl=lWn =63/4,24=15X2 ES= UWR2—>R2= UWI2=6345,26=10X2 PnsR gdy Rw=R P*=E *t=l 26*10,5=1323W    P®r=Rw*P=661,5W

P*,=R1‘11³=264,6W    P_b=R2*Q^391,8W

Zad

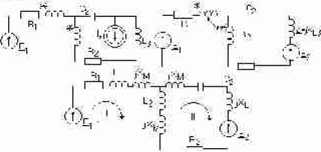
XL3=<BL3 £2=C*jXL3 Zll=Rl+j«BU+XM+<oL2+XM>

Z22=R2łj(XM+01t.2- XM-1/ «C+X1.3) Z12^(toL2+XM) Zll*j_ł.-Z12*kf=El -ZI2*r₍+Z22‘I_u=G2

k .

U^l/T^u^ Vl/Tf„^T Unr*sin³«dt=

■W 1/T fo^T LW2-l/rl^T14* cos2oX)=Vl.'2Tlo^T Urn³ <te=

=V Uirf/ 4TMJm/ 2    Um=100*2=20Q ta=Um/R=4A <ys 1

I=tm/2 1=2A    Uo=100V - rys 2    U=Um/\2=141 -rys 3

Zad

:">(T)

L-!

I I c(t)=20 sinIOOt, Rw=100X2, L=1H, i(t), u(t), p(t>=7 Xr.=cJU=100X2 Um=20V 911=0 U^W2ej° U=14V fc=łl/ Rw+ix₁.=14/100+jl00=0,07-j0,07 1=0,1 9=45°    91= *45° i(t)=0,I4 śnflOOMS⁰)

p(t)=U*I cos 9 - U*I cos{2(0t+9ir+9i)

Zad.

l-.i

*^,JRl

Zad Metoda oczkowa

U ^ ć

-—'YV_._li __

i 'J.-Cs

Xt=2Xc

Zll=Rl+jXU+jXL2-2jXM Z22=S2*jXe+jXL2 Z12=jXL2-jXM

E1=Q*Z11-13*Z12 E2=a*Z22-£3*Z12    0=11+12