3582324702

Adam Zaborski. Wytrzymałość materiałów, semestr 1

Walerowicz Paweł WIL gr. 9 Projekt nr 1

Geometryczna niezmienność układu

Określić geometryczna niezmienność wewnętrzną i zewnętrzną poniższych układów;

Metody:

• Twierdzenie o dwóch tarczach:

WKW geometrycznie niezmiennego połączenia 2 tarcz jest połączenie ich 3 prętami, których kierunki nie przecinają się w jednym punkcie (także niewłaściwym)

1)

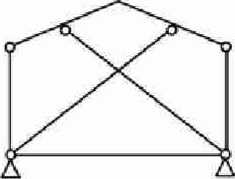
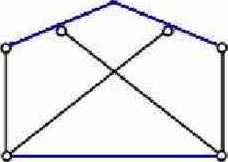
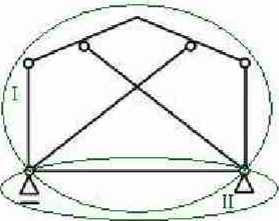
2)

Najpierw zanalizujemy wewnętrzną niezmienność układu.

Tarcze zaznaczone kolorem niebieskim są ze sobą połączone 4 prętami, a ich kierunki nie przecinają się w jednym punkcie, więc zgodnie z twierdzeniem o dwóch tarczach jest to układ wewnętrznie niezmienny.

Do określenia zewnętrznej niezmienności układu również skorzystamy z twierdzenia o dwóch tarczach. Jako jedną z nich przyjmiemy cały układ, którego niezmienność wewnętrzną ustaliliśmy powyżej (I), jako drugą przyjmiemy „Ziemię” - tarcze stworzoną przez nasze podpory (II). Podporę z przesuwem możemy zastąpić pojedynczym prętem, podporę bez przesuwu dwoma, czyli nasze dwie tarcze są połączone trzema prętami - zgodnie z twierdzeniem o dwóch tarczach układ jest zewnętrznie niezmienny.

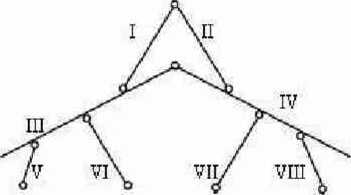
Ponownie zaczniemy od analizy niezmienności wewnętrznej układu. Jednak tym razem nie weźmiemy jednego układu dwóch tarcz, lecz będziemy analizować poszczególny pręty po kolei parami:

•    Pręty I i II łączy jeden przegub (2 pręty)

•    Pręty I i III łączy jeden przegub (2 pręty)

•    Pręty II i IV łączy jeden przegub (2 pręty)

•    Analogicznie jest z pozostałymi parami prętów sąsiadujących (III i V, III i VI, IV i VII, IV i VIII). Prętów niesąsiadujących ze sobą nie rozpatrujemy (są niezależne).

Zgodnie z twierdzeniem o dwóch tarczach w każdym połączeniu „brakuje" jednego pręta by układ był geometrycznie niezmienny - wniosek; układ jest wewnętrznie zmienny.