3582334088

Adam Ślusarczyk

[e-mail]

Y(j2nf)=}[lXf +2)-11C f

n ^1	i RfX(j2xfl n ^
-2 -1	1 2 3
-2)].
n ^1	f.
-2 -1 0 -1	' LiJ^3

Zadanie 7. Znaleźć sygnały o widmach: a) X()2nf), b) YQ2nf).

Zadanie 8. Znaleźć widmo sygnału x(t).

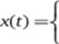
sinr

0

O <n f <0 lubt ^n.

i

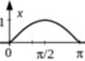
Zadanie 9. Znaleźć widmo sygnału x(f)-

x(0 = (1 -OKO + (2i- l)l(f-1/2) - t l(t-1)

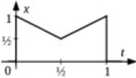
Zadanie 10. Znaleźć widmo sygnału x(f).

x(0 = 11(0 + (1-0K<-1) ⁺ (3-f)l(l-3) + (/—4)l(f—4)

Zadanie 11. Znaleźć transformaty Fouriera sygnałów: xj[t) = e~** i ydt) = sgnf, gdzie a>0, a następnie transformaty Fouriera w sensie granicznym sygnałów: x(f) = 1 i y(f) = sgnf.

Wskazówka. Warto zauważyć, że x(0 = s(t) + s(-t) oraz y(t) = s(t)-s(-t), gdzie

s(f)=e-~l(r).

-r	i i	40 l r	1 - •,
	■	■0
	0 -•1 i!:	1 j<o

0 1 2

Zadanie 4.12. Znaleźć transformaty Fouriera (w sensie granicznym) sygnałów okresowych: a) s(t), b) x(0, c) y(t), d) z(f).

. .    _ -j t -ł-JcT i

s(0=A£rt-),

X(f) = ICf -ł-2/c) -I Xt +2k -t-1),

y( 0 =    |r -ł-2 k),

h

EL

z(t) = y^rxi-\+2k). Wskazówka. Rozwinąć s(t) w szereg Fouriera.

2