3582425897

Zadanie 34. (4 pkt)

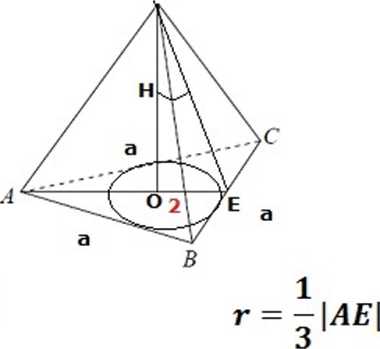
Objętość ostrosłupa prawidłowego trójkątnego ABCS (tak jak na rysunku) jest równa 72. a promień okręgu wpisanego w podstawę ABC tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.

^{V =} 3 P^p H

72= - P_p H 1 a²V3

72 -----H

3    4

1 (4V3)²V3

72 =    ----H

3    4

1 a%/3

r = — 3

1 (4V3)²V3

72= -

3    4

1 48%/3

72 -----H

3    4

48%/3

72 ---H

12

72 = 4\/3 • H

4\/3 tf = 72 72

H =

ay3

T

a\3

2 =-

6

aV3 = 12 12

12 V3

V3 V3

12^3

r =

a =

a =

a =

a = 4\/3

4%/3

18 V3

H = — • — V3 V3

18n/3

H =-

3

H = 6\3

tg(<OSE) = tg(<OSE) =

\OE\

|05|

2

6n/3

,    .    1 V3

tg(<OSE) =i^f

,    , V3

tgliOSE) =—

Minor

wtM*Trtiir W