3582501298

XII. TRÓJKĄTY - gimnazjum

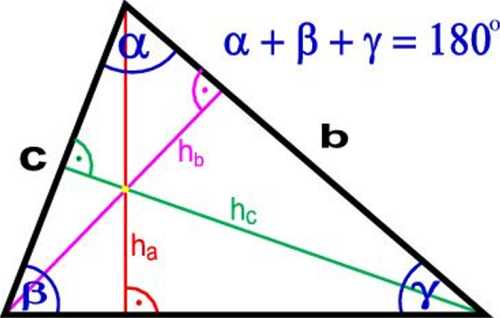
A. TRÓJKĄT DOWOLNY

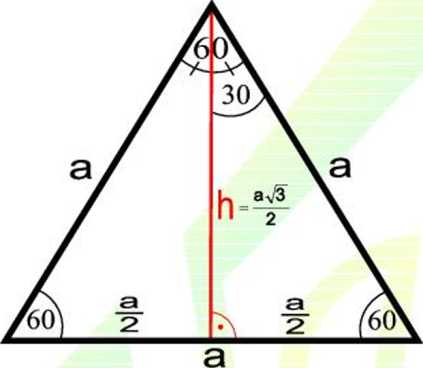
B. TRÓJKĄT RÓWNOBOCZNY

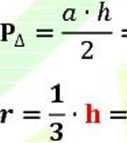
a² ■ V3    a • V3

^{h =} —

aV3    2 aV3

——i /? = —■ h = ——

a

_ a h_a _ b ■ h_h _ c h_c

^A 2 2 2

gdzie:

a, b, c- boki trójkąta

a, fi, y - kąty trójkąta

h_a, hb, h_c - wysokości trójkąta

Pa - pole trójkąta

gdzie:

a -    trójkąta; // - wysokość trójkąta

r - promień okręgu wpisanego w trójkąt R - promień okręgu opisanego na trójkącie

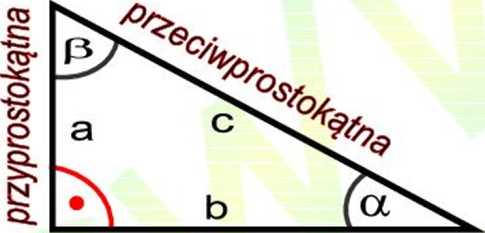
C. TRÓJKĄT PROSTOKĄTNY

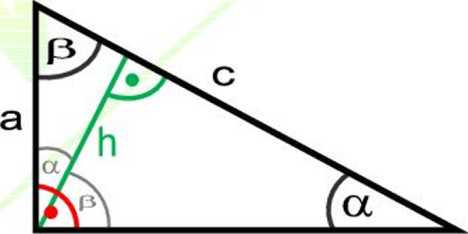
b

przyprostokątna

(1)    Suma kątów ostrych:    a + P = 90°

(2)    Twierdzenie Pitagorasa:    a² + b² = c²

ab c h

(3)    Pole trójkąta:    P_A = —= -y-gdzie:

a, b - długości przyprostokątnych c - długość przeć iwproś to kątnej h - wysokość poprowadzona do boku c

Twierdzenie Pitagorasa dotyczy tylko trójkąta prostokątnego.

A. SZCZEGÓLNE PRZYPADKI TRÓJKĄ TA PROSTOKĄ TNEGO

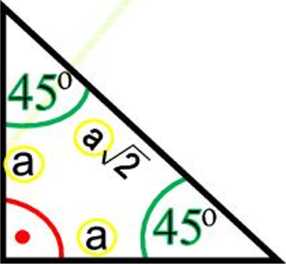
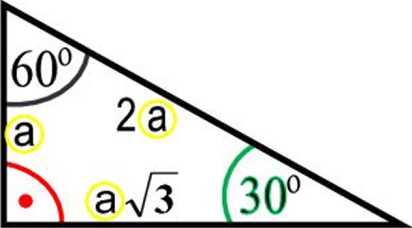
16

O Copyright by Ewa Kędziorc-yk

www. m atem utyka, sosno wiec.pl