1109145229
det(i?,i?2) = det(Ą) det(J?2) = 1 • 1 = +1
Ad (c):
^ „ _ \cO —sO cip —s<p _ cdcip — sOs<p —cOsip — sOcip 1 [ s9 c0 J [ sip cip J [ sOcip + cdsp —s8sp + cdcip
Wykorzystując tożsamości trygonometryczne
cdcip — sOsip = cos (6 + ip) sdcp + cffsip = sin(0 + <p)
otrzymamy rozwiązanie zadania.
10
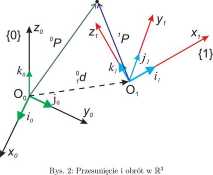
Macierze przekształcenia jednorodnego:
|
R3x3 I d3x, |
obrót przesunięcie | |
|
. /lx3 |filxl |
perspektywa | skalowanie |
Wyszukiwarka
Podobne podstrony:
m8 (2) Rozdział 2 Wielomian charakterystyczny macierzy: w(A) = det(v4 - A/„) Wartość własna macierzy
186 LA VERTU ET LE PRĆCEPTE 2«, 108, 3, ad 4). La justice, au contraire, dont 1’acte est d’etre ad a
skanuj0027 • tpiiWJDia. ętĄ ujL«k3dU3t «Mc^w«u.e -eAern^jjJiytcŁi voatooatoił.e joJc co so^tetisotJU
skanuj0027 • tpiiWJDia. ętĄ ujL«k3dU3t «Mc^w«u.e -eAern^jjJiytcŁi voatooatoił.e joJc co so^tetisotJU
Obraz (828) 9>. 2 . £>An>Ł : Z A 1 €> = SC + D ^ , 3 I-So i«? 4^~*< l 1 Ą o i A &
IMG&63 «***** s*=o,6 _ <D,Cfl~ n ----- co z /f+o,c<Z /SO,*,-!.- m mSi SI 1
skanowanie0002p £+ = - + 4L l ł. * (coi -fi>*) —&„&>*(**-A^Co^(ęA-
skanuj0019 3 CO» SO dMH C*—* *•*»«-A-teloj IktJlwLi °r a. •J 3 *frr—*»«€ • -
10 (8) IM +>i < W Ul 33~ r,5T - od ,llx —Ś^CbSai^^co^ ł"0 “O-Jbi -i,ftt
a .wiem". Dzięki AD to, co się nam „wydaje", może się okazać nieprawdą albo zyskać empiryc
Mierniki cyfrowe I 11 11 11 II UJ. U. U AX = Ap+Ad a., „ A. =——X p 100 A -M-°x - X Arf
Zabawa z ekologią25 26(1) •„idsz wszystko to, Ańre uWesc S „„ctości co i^st c 1 Park jest ostoją prz
więcej podobnych podstron