1060440354

3) przy większej liczbie zależności zaznaczanych na jednym wykresie należy zastosować rozróżnienie oznaczeń, zarówno do punktów pomiarowych (zróżnicowanie kolorów lub kształtu punktów), jak i do linii przedstawiających zależności (zróżnicowanie kolorów lub deseni linii). Każda z krzywych powinna być opisana.

b)

a)

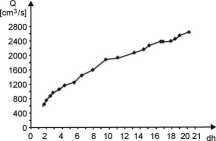
[cm]

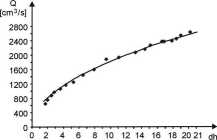
[cm]

Rys. 4.2.3. Przykłady krzywych reprezentujących analizowaną zależność: a) wykonana nieprawidłowo, b) wykonana prawidłowo

4.3. Przedstawianie danych za pomocą równań matematycznych.

Aproksymacja zależności funkcyjnej metodą najmniejszych kwadratów

Bardzo wygodne, a niekiedy konieczne, jest przedstawienie związku między analizowanymi wielkościami w postaci zależności funkcyjnej. Określana jest wówczas analityczna postać relacji między rozważanymi zmiennymi. Równanie poszukiwanej funkcji, w zależności od sposobu jej określania, może mieć charakter równania teoretycznego, czyli otrzymanego na drodze analizy teorii badanego zjawiska, lub równania empirycznego, czyli uzyskanego na podstawie wyników pomiaru wartości analizowanych zmiennych. W obu przypadkach konieczne jest wyznaczenie wartości stałych występujących w tych równaniach, a dla równania empirycznego dodatkowo należy określić postać tej zależności. Żąda się przy tym, aby równanie przedstawiało uzyskaną w efekcie pomiarów' zależność możliwie najlepiej. Poszukiwanie funkcji odzwierciedlającej analizowaną relację jest określane mianem aproksymacji, natomiast uzyskana w jej efekcie funkcja nosi nazwę funkcji aproksymującej.

Postać ogólną poszukiwanego równania funkcji aproksymującej określa się na podstaw ie własnego doświadczenia lub przez analizę układu punktów (stanowiących podstawę aproksymacji) na wykresie i analogię kształtu zależności do znanych postaci funkcji. Z kolei stale występujące w równaniu funkcji należy dobrać tak, by uzyskać możliwie najlepsze dopasowanie wykresu funkcji do tego układu punktów. Istotne jest zatem kryterium, które pozwoli ocenić jakość tego dopasowania i wybrać obiektywnie najlepsze.

Najczęściej stosowanym kryterium oceny zgodności między funkcją aproksymującąy = f(x) a aproksymowanym układem punktów jest kryterium najmniejszego błędu kwadratowego.

Niech będzie dany zbiór Npunktów o współrzędnych (x,,y,) (i = I...N), których układ należy aproksymować zależnością o wybranej postaci y = f(x), przy czym w funkcji f występuje k stałych a_u

11