4037602954

6 1. Wiadomości wstępne

przerwać proces iteracji a otrzymana wartość Xi jest wystarczająco dobrym przybliżeniem. W zależności od wartości wyrażenia warunkowego, w pętli whileO będzie wykonywana iteracja aż do osiągnięcia zadanej dokładności:

while (std::fabs(x * x - a) > e)

Może się zdarzyć, że proces będzie rozbieżny lub kryterium precyzji zbyt wygórowane. Należy zadbać o kontrolę liczby iteracji, zazwyczaj ustawiamy licznik pętli i w momencie, gdy liczba iteracji przekroczy ustalona granicę, zatrzymujemy obliczenia.

Rozwiązując zadanie metodami numerycznymi spotkamy się z przypadkami tak zwanej niestabilności numerycznej. Mówiąc nieprecyzyjnie niestabilność numeryczna polega na nieoczekiwanym zachowaniu się rozwiązania. Na przykład, zmieniając jakiś parametr w metodzie numerycznej, otrzymujemy całkowicie inne rozwiązanie. Rozważmy klasyczny przykład niestabilności numerycznej z podręcznika R. Hor-necka. Chcemy rozwiązać równanie różniczkowe postaci:

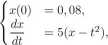
(1.9)

przy pomocy metody Runge-Kutty 4 rzędu (numeryczne metody rozwiązywania równań różniczkowych zwyczajnych zostaną omówione w dalszych rozdziałach) w przedziale 0 < t < 5. Przy warunkach początkowych (x(0) = 0.08) dokładne rozwiązanie jest znane i ma postać:

— t² + 0,41 + 0,08,

X —

(1.10)

W metodzie Runge-Kutty zasadniczym parametrem jest krok iteracji. Jeżeli zastosujemy krok At = 0,1, to dostaniemy prawie dokładne rozwiązanie dla 0 < t < 1,7. Powyżej wartości t = 1,7 rozwiązanie numeryczne drastycznie odbiega od rozwiązania prawdziwego (zobacz Rysunek 1.4). Zmiana kroku iteracji rozwiązania numerycznego na At — 0,01 przesunie granicę dobrego rozwiązania do wartości t — 3,7.

Niestabilność numeryczna może sprawiać wiele kłopotów przy rozwiązywaniu zadań metodami numerycznymi. W opisanym przypadku mogliśmy porównać nasze rozwiązanie numeryczne z rozwiązaniem dokładnym. W praktyce rzadko znamy rozwiązanie analityczne (nie ma sensu rozwiązywanie zadania metodami numerycznymi, gdy znamy dokładne rozwiązanie), stosujemy metody numeryczne, gdy inne techniki są nieosiągalne. Dlatego należy wykonać wiele testów rozwiązań numerycznych, aby mieć pogląd na dokładność rozwiązania. W opisanym przykładzie niestabilności numerycznej rozwiązanie problemu jest znane - do tego typu równań różniczkowych metoda Runge-Kutty się nie nadaje. Rekomendowana jest metoda Geara.