4037602955

1.3. Błędy w metodach numerycznych 7

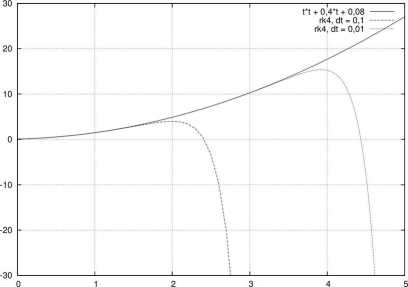
Rysunek 1.4: Przykład niestabilności numerycznej, rozwiązywanie równania różniczkowego.

1.3 Błędy w metodach numerycznych

Rozwiązując zadania metodami numerycznymi popełniamy błędy. Występujące błędy są powodowane wieloma czynnikami. Doskonałe omówienie błędów występujących w analizie numerycznej znajduje się w monografiach A. Ralstona (Wstęp do analizy numerycznej) oraz A. Bjorcka i G. Dahląuista (Metody numeryczne). Niektóre typy błędów są łatwe do usunięcia, inne ewentualnie można wyeliminować lub zredukować. Ważne jest jednak, aby zdawać sobie sprawę z natury błędów, jakie mogą powstać w wyniku obliczeń przeprowadzanych przy pomocy komputerów. A. Ralston wyróżnia trzy główne źródła błędów:

•    grube błędy i pomyłki,

•    błędy metody (obcięcia),

•    błędy zaokrąglenia.

Pomyłki zdarzają się zawsze, na przykład wprowadzając dużą ilość danych, można źle wprowadzić konkretną liczbę. Uważne, ponowne sprawdzenie wprowadzonych danych może wyeliminować pojawienie się tego typu pomyłki. Błędy metody spowodowane są faktem, że:

•    Korzystając z kilku początkowych składników szeregu Taylora. Szacowanie wartości funkcji elementarnych (np. e^x) - zadanie jest rozwiązywane nie w postaci dokładnej, ale w postaci przybliżonej.