4130648953

KAPITAŁ LUDZKI If !

NARODOWA STRATEGIA SPÓJNOŚCI

UNIA EUROPEJSKA

EUROPEJSKI FUNDUSZ SPOŁECZNY

Projekt współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Rozważmy system liniowy stacjonarny 5j

x(t) = Ax(t) + Bu{t)    (3.3)

y(0 = Cx(t)

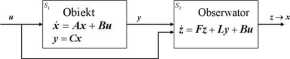
Będziemy szukać obserwatora stanu x systemu (3.3) w postaci liniowego systemu stacjonarnego S₂ postaci

i(t) = Fz(t) + Ly(t) + Bu(t)

(3.4)

Rys.3.1 Obiekt (jako system liniowy i stacjonarny) S\ połączony z układem S₂ jako obserwatorem.

W tym celu odejmijmy równania (3.4) i (3.3) stronami: i(t) - x(t) = Fz(t) - (A - LC)x(t)

Przyjmując macierz L tak, aby F = A LC mamy i(‘)-x(t) = F(z(t)-x(t))

Definiując teraz błąd odtwarzania obserwatora jako e(t) = z(l) - x(t) otrzymujemy równanie błędu

e(t) = Fe{t)    (3.5)

zapewniające zbieżność e(t) —> 0 czyli z(t) —> x(/) (gdy / —> oo) na mocy właściwego wyboru wartości własnych macierzy F.

Dokładność asymptotycznego odtwarzania wektora stanu x zależy, więc od wartości własnych macierzy F oraz warunków początkowych x(0) i z(0) . Wektor z(t) będzie odtwarzał stan x(t) tym dokładniej im większe będą moduły ujemnych części rzeczywistych wartości własnych macierzy F. Projektując obserwator należy zatem przyjąć macierz L z uwzględnieniem tych faktów.

Oznaczając z(t) - x(t) równanie obserwatora (3.4) z reguły zapisujemy w postaci

x(t) = Ax(t) + Bu + L(y(t)-Cx(t)) .    (3.6)

W tej formie pokrywa się ono z równaniem filtru Kalmana, jednak w przypadku filtru znalezienie macierzy wzmocnienia L, jako wynik procesu optymalizacji stochastycznej, jest znacznie bardziej skomplikowane.

Projekt „Rozwój i promocja kierunków technicznych w Akademii Morskiej w Szczecinie" Akademia Morska w Szczecinie, ul. Wały Chrobrego 1-2, 70-500 Szczecin 16