4544140698

VII Toruńska Letnia Szkoła Matematyki i Informatyki

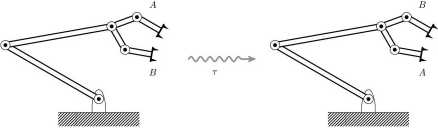
Obrót po łuku okręgu w płaszczyźnie prostopadłej do płaszczyzny kartki przeprowadzi robota z jednej pozycji do drugiej. Który z dwóch możliwych wyborów kierunku obrotu jest właściwy?

Geometrie nieeuklidesowe, skąd się wzięły, i co o nich dziś wiadomo

dr hab. Marek Kord os, prof. UW,

Uniwersytet Warszawski

Geometria dorycka, pojęcia pierwotne, automorfizmy, znaczenie cywilizacyjne. Elementy jako wzór ścisłości rozumowań. Program Proklosa dowodu V postulatu. Geometria absolutna i pseudodowody V postulatu. Geometria hiperboliczna i jej twórcy. Modele geometrii hiperbolicznej i jej równoważność z euklidesową. Gauss i geometria wewnętrzna. Theorema egregium. Krzywizna a miara. Geometria Riemanna. Helmholtz i aprzy-rodniczość matematyki. Ogólna Teoria Względności. Jednorodna metryza-cja rozmaitości. Marków i nieklasyfikowalność rozmaitości wysokowymia-rowych. Thurston i hipoteza geometryzacyjna. Potoki i Perelman.

Geometria rzutowa i jej dyscypliny pochodne

dr hab. Marek Kordos, prof. UW,

Uniwersytet Warszawski

Struktury dwusortowe. Aksjomatyka geometrii rzutowej i przegląd modeli. Dualność syntaktyczna i semantyczna. Własności topologiczne płaszczyzny rzutowej. Rzuty, przekształcenia rzutowe, kolineacje i korelacje. Konfiguracje Desarguesa i Pappusa-Pascala, nowa symetria. Podstawowe Twierdzenie Geometrii Rzutowej. Korelacje biegunowe, stożkowe. Twierdzenie Seydewitza i konstrukcja stycznej samą linijką. Twierdzenia Ste-inera, Braikenrigde'a-Maclaurina, Pascala-Brianchona i ich uogólnienia. Współrzędne bary centry czne i droga do geometrii algebraicznej. Cayley i geometria czteroabsolutna. IV problem Hilberta, geometrie Minkowskiego i Hilberta. Ciała cechujące i twierdzenie Fritza Johna.