5987092972

maksymalnie 6 zmiennych. Tablica Karnaughta jest tablicą, której kolejne wiersze i kolumny są opisane w kodzie Graya, co zapewnia nam sąsiadowanie ze sobą tych jedynek (bądź zer) funkcji, które podlegały będą sklejeniu. Przykładowe tablice Karnaught przedstawia rys. 12.

	0	?	£	0	1	JŚsfoO		0111 10
0	0	1	30	0	1	©o	0	1	3	2
1	2	3	01	2	3	01	4	5	7	6
			11	6	7	11	12	13	15	14
			10	4	5	10	8	9	11	10

crtJfooornio

000	0	1	3	2
001	4	5	7	6
011	12	13	15	14
010	8	9	11	10
110	24	25	27	26
111	28	29	31	30
101	20	21	23	22
100	16	17	19	18

Rys. 12. Tablice Karnaught: a) dwóch zmiennych; b) trzech zmiennych; c) czterech zmiennych; d) pięciu zmiennych

Przykład

Zaprojektować schemat układu opisanego funkcją

/(d, c, b, a) = |][0,1,2,5,8,9,10,13,15, (3)],wykorzystując tylko elementy NAND.

Pierwszym etapem będzie polegał na przeniesieniu wartości funkcji /(d,c,b,a) do tablicy Karnaughta. Następnie musimy dokonać minimalizacji poprzez poszukiwanie minimalnej postaci sumy (zakreślanie jedynek- przykład a), bądź przez poszukiwanie minimalnej postaci iloczynu (zakreślanie zer- przykład b). a)    b)

	00	»	u
00	. J			l_.
01	0	1	0	0
11	0	DI	■1	0
■"	-4	*	“	4^

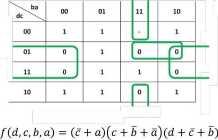
a) W przypadku gdy dysponujemy minimalną postacią sumy (alternatywa) dokonujemy: - podwójnej negacji równania i eliminacji alternatywy przez zastosowanie prawa de Morgana:

/(d, c, b, a) = ća + ba + dca = ca + ba + dca = ca -ba - dca