6352194258

MATURA 2015 Z MATEMATYKI

NIE TAKI DIABEŁ STRASZNY...

POZIOM PODSTAWOWY

We wtorek 5 maja abiturienci szkól licealnych pisali maturę z matematyki na poziomie podstawowym po raz pierwszy wedle nowych zasad. Po „groźnych" zapowiedziach minister edukacji na temat nowej matury oraz po trudnej maturze próbnej w grudniu „matematyczny diabeł” okazał się być nie taki straszny jak go malowali. Aż 50% wszystkich punktów maturzysta mógł zdobyć z zadań zamkniętych, które uchodzą za dość proste. Nie zabrakło standardowych zadań takich jak rozwiązanie nierówności kwadratowej czy obliczenie powierzchni całkowitej graniastosłupa. Trzeba jednak przyznać, że nawet standardowe zadania były nieco trudniej sformułowane i nie stanowiły zupełnej „sztampy maturalnej” jak to się zdarzało na maturach do tej pory. Nie zabrakło tradycyjnie zadań „na dowodzenie”. Zgodnie z naszymi przewidywaniami były dwa trudniejsze zadania tego typu: dowód geometryczny i dowód algebraiczny. Dla wielu osób okazało się być trudnym zadanie z biletami, gdzie warto było posłużyć się wzorem na prawdopodobieństwo sumy dwóch zdarzeń. Podsumowując, matura podstawowa w tym roku była łatwiejsza niż matura próbna, jednak nie była banalna.

Jak co roku umieszczamy tabelkę porównawczą, która pokazuje na wybranych przykładach, że praktycznie każde zadanie, które pojawiło się na tegorocznej maturze ma swój odpowiednik w materiałach, sprawdzianach lub maturach próbnych przygotowanych przez Collegium Novum.

ODPOWIEDNIKI TEGO ZADANIA MATURALNEGO, UMIESZCZONY W MATERIAŁACH COLLEGIUM NOVUM

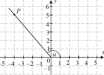
zaznaczonego n

ZESTAW 14. ZADAŃ TESTOWYCH COLLEGIUM NOTOM.

adanie 28. informacji	awartych rys
k. tg/? = 3
a. tg/? = -3	M	Kk .
=• tg/> = 3
, 1

PRZYKŁAD ZADANIA Z ..NOWEJ” MATURY PODSTAWOWEJ 2015	ODPOWIEDNIKI TEGO ZADANIA MATURALNEGO, UMIESZCZONY W MATERIAŁACH COLLEGIUM NOVUM
MATURA MAJ 2015. Zadanie 26.	MATERIAŁ COLLEGIUM NOVUM. WYKŁAD 11.
Rozwiąż nierówność 2x^2-4x>(x + 3)(x-2) .	Zadanie 15. a)    (.*-2X*+ 3) > (*-2X2x+ 5); b)    (r-4)^J+(.*-4X*+2)>0.

ODPOWIEDNIKI TEGO ZADANIA MATURALNEGO, UMIESZCZONY W MATERIAŁACH COLLEGIUM NOYUM

MATERIAŁ COLLEGIUM NOTOM. WYKŁAD 3

że dla każdej liczby rzeczywistej X ażdej liczby rzeczywistej J> prawdzii erówność 4x² -8iy + 5y^! źO .

PRZYKŁAD ZADANIA Z ..NOWEJ" MATURY PODSTAWOWEJ 2015	ODPOWIEDNIKI TEGO ZADANIA MATURALNEGO, UMIESZCZONY W MATERIAŁACH COLLEGIUM NOVUM
	MATERIAŁ COLLEGIUM NOVUM. WYKŁAD 10.
Oblicz najmniejszą i największą wartość funkcji kwadratowej f(x) = x^2-6x + 3 w przedziale (0,4).	Zadanie 45. Oblicz najmniejszą i największą wartość funkcji kwadratowej /(*) = (2r+l)(r-2) w przedziale (-2,2).

PRZYKŁAD ZADANIA Z „NOWEJ” MATURY PODSTAWOWEJ 2015	ODPOWIEDNIKI TEGO ZADANIA MATURALNEGO, UMIESZCZONY W MATERIAŁACH COLLEGIUM NOVUM
	MATERIAŁ COLLEGIUM NOVUM. WYKŁAD 21.
Wysokość graniastosłupa prawidłowego graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem, którego cosinus jest równy - . Oblicz pole	W graniastosłupie prawidłowym czworokątnym przekątna podstawy ma długość 8 cm i tworzy z przekątną ściany bocznej, z którą ma wspólny wierzchołek kąt, którego cosinus jest równy | . Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.

POZIOM ROZSZERZONY

Trzy dni po napisaniu matury podstawowej z matematyki abiturienci zmierzyli się z poziomem rozszerzonym. Dla wielu osób zadania na poziomie rozszerzonym okazały się być nie lada wyzwaniem. Poziom trudności zadań był dosyć wysoki, jednak nic przekraczał tego, na co przygotowała nas matura próbna w grudniu. Zatem, tak jak zapowiadaliśmy na wykładach w Collegium Novum, pojawiły się zadanie „na dowodzenie" z geometrii płaskiej, zadanie z wyznaczeniem stycznej do wykresu funkcji, zadanie na prawdopodobieństwo całkowite oraz zadanie optymalizacyjne. Wiele osób „poległo" na zadaniu z wielomianem, którego pierwiastki tworzyły ciąg arytmetyczny o różnicy 3. Nie było to jednak, jak wiele osób sądzi, zadanie „rachunkowe" tylko zadanie „na spostrzegawczość". Tak jak przewidywaliśmy, zadań testowych oraz „kodowanych” było bardzo mało. I już tradycyjnie głównym wrogiem maturzystów był czas, a dokładniej jego brak...

Przyjrzyjmy się poniżej tabeli porównawczej, która pokazuje na wybranych przykładach, że praktycznie każde zadanie, które pojawiło się na tegorocznej maturze ma swój odpowiednik w materiałach, sprawdzianach lub maturach próbnych przygotowanych przez Collegium Novum.

ODPOWIEDNIKI TEGO ZADANIA MATURALNEGO, UMIESZCZONY W MATERIAŁACH COLLEGIUM NOYUM

MATURA MAJ 2015. Zadanie 8.

Udowodnij, że dla każdej liczby rzeczywistej prawdziwa jest nierówność x*-jf -2x+5>0.

Wykaż, że równanie ż^+ó-r*-jedno rozwiązanie.

ODPOWIEDNIKI TEGO ZADANIA MATURALNEGO, UMIESZCZONY W MATERIAŁACH COLLEGIUM NOYUM

MATURA MAJ 2015. Zadanie 16.

Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie 20. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.

COLLEGIUM NOTOM.

lozpatrujemy wszystkie stożki wpisane w ku i promieniu 6. Jaka jest wysokość stożka c lajwiekszej objętości?

PRZYKŁAD ZADANIA Z „NOWEJ” MATURY ROZSZERZONEJ 2015

ODPOWIEDNIKI TEGO ZADANIA MATURALNEGO, UMIESZCZONY W MATERIAŁACH COLLEGIUM NOYUM

MATURA M

ale

MATERIAŁ COLLEGIUM NOTOM. WYKŁAD 26.

i 5 kul czarnych, a w drugiej urnie 7 kul białych i 2 kule czarne. Losujemy jedna kule z pierwszej urny, przekładamy ja do urny drugiej i dodatkowo dokładamy do urn; drugiej jeszcze dwie kule tego samego koloru, co wylosowana kula. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego obie kule wylosowane z drugiej

imy b

ą 29.

W pierwszej urnie znajdują Sie 2 kule białe i 4 czarne, zaś w drugiej urnie 4 kule czarne i 2 białe. Losujemy z urny pierwszej jedna kule, i nie oglądając jej, wkładamy ja do urny drugiej. Następnie z urny drugiej losujemy dwie k prawdopodobieństwo, ż< beda różnych kolorów.

Oblicz

PRZYKŁAD ZADANIA Z ..NOWEJ” MATURY ROZSZERZONEJ 2015	ODPOWIEDNIKI TEGO ZADANIA MATURALNEGO, UMIESZCZONY W MATERIAŁACH COLLEGIUM NOVUM
MATURA MAJ 2015. Zadanie 6.	MATERIAŁ COLLEGIUM NOTOM. WYKŁAD 26.
Oblicz granicę limf^lln+6" ^+ 5 2"^2 + 2" ^+ 0 6n^5 +1 Sn^2 - 4 J	Oblicz granicę lim ^ ^+ ^ ^+ ^jj ■

oiałe.

PRZYKŁAD ZADANIA Z ..NOWEJ" MATURY ROZSZERZONEJ 2015	ODPOWIEDNIKI TEGO ZADANIA MATURALNEGO, UMIESZCZONY W MATERIAŁACH COLLEGIUM NOVUM
MATURA MAJ 2015. Zadanie 12.	MATERIAŁ COLLEGIUM NOTOM. WYKŁAD 26.
Funkcja / określona jest wzorem f(x) = x‘-2x^2 + \ dla każdej liczby rzeczywistej X. Wyznacz równania tych stycznych do wykresu funkcji /, które są równoległe do prostej o równaniu y = 4x .	Zadanie 19. Styczna do wykresu funkcji f jest równoleqła do prostej m. Wyznacz współrzędne punktu (punktów) styczności P. a)    f(x) = -x^2-2x. m\y = 2x-i b)    /(*) = **-3r, nr. 9r-y + 2015 = 0

Koordynator pionu matematycznego Collegium Novum Grzegorz Pałgan.