6352200765

MATEMATYKA Scenariusz lekcji dla klasy VI

TEMAT: Skala i plan.

Powiązanie z wcześniejszą wiedzą

Uczniowie:

znają pojęcie skali

znają i zamieniają jednostki długości

określają rzeczywistą wielkość obiektu na podstawie rysunku sporządzonego w skali

-    rysują obiekty w podanej skali

odczytują potrzebną informację z prostego planu

Cele lekcji:

-    rozwiązywanie zadań związanych ze skalą planu lub mapy

Cele sformułowane w języku ucznia:

Po dzisiejszej lekcji:

-    będziesz rozumiał pojęcie skali na planie (mapie)

-    będziesz umiał zastosować pojęcie skali w zadaniach z wykorzystaniem mapy bądź planu.

-    będziesz umiał wykorzystać pojęcie skali w sytuacji rzeczywistej np. do obliczenia rzeczywistej długości trasy przed wyjazdem na wakacje.

Nacobezu (kryteria oceniania):

wyjaśnisz słownie, co określa skala mapy (planu) zamienisz skalę liczbową na mianowaną

obliczysz rzeczywistą odległość między obiektami na podstawie skali i danej odległości na mapie (planie)

określisz skalę, gdy dane są wymiary rzeczywiste i wymiary na planie (mapie) obliczysz odległość na mapie (planie), na podstawie skali i rzeczywistej odległości w terenie

odległości rzeczywiste zapiszesz we właściwych jednostkach.

Kluczowe pytanie dla uczniów:

Jak myślisz, czy plan naszej klasy w skali 1:100 zmieści się na kartce formatu A4? Uzasadnij.

Metody:

Aktywizujące: rozmowa dydaktyczna, „dyskusja w parach”, „samoocena koleżeńska”, gry dydaktyczne: PRAWDA FAŁSZ, DOMINO MATEMATYCZNE Praktyczne:    ćwiczenia praktyczne z wykorzystaniem planu i mapy.

Programowe:    praca z użyciem podręcznika programowego.

Na zajęciach lekcyjnych zastosowano element}* oceniania kształtującego.

Formy pracy: indywidualna, z całą klasą, grupowa

Środki dydaktyczne: podręcznik dla klasy VI Matematyka 2001, mapa Polski, atlasy geograficzne, plany miasta Dąbrowa Górnicza, kolorowe kartoniki do gry PRAWDA FAŁSZ, kolorowe kartoniki do „metody świateł”, kolorowa kreda, magnesy, karty pracy ucznia.

PRZEBIEG ZAJĘĆ:

Faza wprowadzająca

I.    Czynności organizacyjne:

sprawdzenie obecności sprawdzenie pracy domowej

- rozdanie kart pracy, planów miasta Dąbrowa Górnicza.

II.    Część wstępna

1.    Pytanie motywujące: Czy potraficie wymienić przykłady zastosowania skali w życiu codziennym?

2.    Przypomnienie podstawowych wiadomości o skali:

(rzucanie piłeczką - osoba, która złapie piłeczkę odpowiada na pytanie)

Kiedy stosujemy skalę? Co ona określa?

Co oznacza skala 1:2, 2:1, 1:1?

Czym różni się mapa od planu?

(W odróżnieniu od mapy, plan nie uwzględnia krzywizny Ziemi i różnic wysokości na danym terenie. Najczęściej można spotkać plany miast w skalach 1: 10 000 lub 1: 5000. Plany mieszkań sporządza się zwykle w skalach 1: 100 lub 1:100)

3.    Zadanie pytania kluczowego:

Jak myślisz, czy plan naszej klasy w skali 1:100 zmieści się na kartce formatu A4? Uzasadnij.

O odpowiedź poprosimy pod koniec lekcji.

4.    Zapoznanie uczniów z tematem lekcji oraz celami sformułowanymi w języku ucznia. Podanie nacobezu.

Faza realizacyjna

1. Wyjaśnienie, co oznacza skala na planie/mapie.

W klasie wisi mapa Polski i plan Dąbrowy Górniczej.

- Co to znaczy, że mapa wykonana została w skali 1: 50 000 ?

-    Jak obliczymy, jakiej odległości w terenie odpowiada odcinek, który na mapie ma długość 7 cm, 1 dm ?

7 cm na mapie to 7 • 50 000 cm w terenie

1 dm na mapie to 10 • 50 000 cm = 500 000 cm = 50 000 dm w terenie

2.    Rozwiązywanie zadań dotyczących skali.

Wspólne rozwiązanie zadań 1 - 3 z karty pracy ucznia.

Zadanie 1. Podaj ilu metrom i ilu kilometrom w terenie odpowiada 1 cm na mapie o skali: a) 1 : 300 000    b) 1 : 15 000

Zadanie 2. Podaj w jakiej skali wykonano mapę, jeżeli odległość między dwoma miejscowościami na mapie wynosi 6 cm, a w rzeczywistości 180 km.

Zadanie 3. Jaka jest rzeczywista odległość między miastami, które na mapie o skali 1 : 200 000 są odległe o 5,5 cm.

3.    Analizowanie, jak zmienia się pole prostokąta narysowanego w skali.

Wspólne rozwiązanie zadania 1 ze strony 160 z podręcznika.

Na rysunku przedstawiono fragment planu centrum Krakowa. Rynek Główny w Krakowie jest na tym planie kwadratem o boku 2 cm. Jaka jest jego rzeczywista powierzchnia?

W jakiej skali wykonano plan Krakowa?

-    Co oznacza skała 1:10 000 na tym planie?

-    Jaka jest rzeczywista długość boku tego kwadratu?

W jaki sposób należy obliczyć rzeczywistą powierzchnię Rynku Głównego? Ile to m?, km²?

-    Czy można najpierw obliczy powierzchnię Rynku Głównego na planie, a następnie wynik pomnożyć przez skalę?

(Należy zwrócić uwagę uczniów, że powierzchnia nie zmienia się w taki sam sposób jak długość, więc nie można obliczyć pola prostokąta na planie mapie, a potem pomnożyć je przez 10 000. Najłatwiej wytłumaczyć ten fakt rysunkiem o prostej skali np. 1:2. Wówczas widać wyraźnie, że prostokąt o długości i szerokości 2 razy mniejszej ma powierzchnię cztery razy mniejszą.)

4.    Rozwiązywanie zadań z wykorzystaniem planu miasta.

Podział uczniów na dwie grupy (indywidualizacja pracy) i samodzielne rozwiązanie zadań z wykorzystaniem planu miasta Dąbrowa Górnicza.

Nauczyciel kontroluje pracę uczniów i w razie potrzeby wyjaśnia wątpliwości. (Zastosowanie „metody świateł”: jeśli uczeń ma problemy, pokazuje światło żółte lub czerwone.)

5.    Odpow iedź na pytanie kluczowe - wypowiedzi uczniów.

Uczniowie muszą najpierw oszacować wymiary sali lekcyjnej, a następnie każdy wymiar prostopadłościanu zmniejszyć 100 razy. Na końcu porównują wymiary sali w skali z wymiarami kartki formatu A4.

6.    Wykorzystanie obliczeń zw iązanych ze skalą w^r sytuacji rzeczywistej.

-    Jaka informacja nie została podana, a jest niezbędna do rozwiązania zadania?

• Uczniowie pracując w grupach 2 - osobowych rozwiązują zadanie 5 z karty pracy, korzystają z atlasu geograficznego. Zastosowanie metody „dyskusja w parach”.

■ Ocena pracy - sąsiednie grupy wymieniają się rozwiązaniem zadania i na podstawie ustalonego schematu oceniania dokonują oceny koleżeńskiej (ocena kształtująca).

Faza podsumowująca

1. Gra dydaktyczna „PRAWDAFAŁSZ”

Uczniowie poprzez podniesienie kolorowych kartoników (żółty - PRAWDA, czerwony -FAŁSZ) odpowiadają napytania zadawane przez nauczyciela:

■    Skala 1 : 7000 oznacza, że odległość w terenie jest 7000 razy większa niż na mapie

/PRAWDA/

■    Jeśli 1 cm na mapie odpowiada 2 km w terenie, to 2,5 cm na mapie odpowiada 4,4 km

w terenie    /FAŁSZ/

■    Jeśli 1 cm na mapie odpowiada 6 km w terenie, to skala mapy wynosi 1 : 600 000.

/PRAWDA/

■    Obszar na mapie w skali 1 : 300 jest zawsze mniejszy niż na mapie w skali 1 : 3000.

/FAŁSZ/

2.    Podsumowanie - zdania podsumowujące:

■    Dziś nauczyłem się, że ...

■    Osiągnąłem założony cel, ponieważ ...

■    Zaskoczyło mnie, że ....

3.    Zadanie i omówienie pracy domowej.

Zadanie 6 z karty pracy

Domino matematyczne (indywidualizacja pracy) Dla chętnych: zadanie 7 z karty pracy

Notatki i dodatkowe ćw iczenia:

Dla uczniów, którzy wykonali poprawnie wszystkie zadania polecenie wymyślenia zadania, które wykorzystuje pojęcie skali w praktyce.

KARTA PRACY UCZNIA Skala i plan - ćwiczenia utrwalające

Zadanie 1. Podaj ilu metrom i ilu kilometrom w terenie odpowiada 1 cm na mapie o skali: a) 1 : 300 000    b) 1 : 15 000

Zadanie 2. Podaj w jakiej skali wykonano mapę, jeżeli odległość między dwiema miejscowościami na mapie wynosi 6 cm, a w rzeczywistości 180 km

Zadanie 3. Jaka jest rzeczywista odległość między miastami, które na mapie o skali

Zadanie 5

Wyobraź sobie, że za 2 tygodnie wyjeżdżasz na wakacje do Sopotu. Wiesz, że Twój samochód spala 6,5 litra benzyny na 100 km. Ile litrów tego paliwa musisz wlać do baku, żeby dojechać na miejsce bez tankowania?

Skala 1 :2000

Zadanie 6

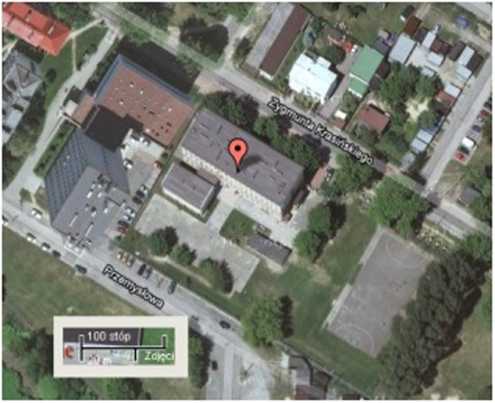
Zdjęcie satelitarne przedstawia Szkołę Podstawową nr 8 w Dąbrowie Górniczej wraz z jej najbliższym otoczeniem. Korzystając z podanej skali oblicz:

a)    długość fragmentu ulicy Z. Krasińskiego

b)    powierzchnię boiska do piłki nożnej

Zadanie 7

W jakiej skali narysowano 2 1 karton mleka „...” w gazetce reklamowej sklepu Real?