6352200768
MATEMATYKA Scenariusz lekcji dla klasy V
Dział: Pola figur płaskich.
TEMAT: Pole rombu
Powiązanie z wcześniejszą wiedzą
Uczniowie:
znają terminologię dotyczącą równoległoboku - podstawa, wysokość, przekątne rombu znają sposób obliczania pola równo ległoboku (w tym również rombu), przy danej długości podstawy i wysokości opuszczonej na tą podstawę
Cele lekcji:
Oblic zanie pola rombu.
Cele sformułowane w języku ucznia:
Po dzisiejszej lekcji:
- będziesz potrafił obliczyć pole czworokąta o prostopadłych przekątnych
wykorzystać obliczanie pola rombu w sytuacji rzeczywistej np. do obliczenia kosztu płytek w kształcie rombu, potrzebnych do wyłożenia nimi podłogi.
Nacobezu (kryteria oceniania):
- podasz dwa spo soby oblic zenia pola kwadratu i rombu
- obliczysz pole rombu (kwadratu), znając długości jego przekątnych
- obliczysz długość jednej z przekątnych rombu (kwadratu), znając jego pole i długość drugiej przekątnej
- narysujesz romb, znając długości jego przekątnych
- narysujesz romb o podanym polu
Kluczowe pytanie dla uczniów:
Wyobraź sobie, że podłogę w Twoim pokoju wykładamy drewnianymi klepkami w kształcie rombu. Jak sądzisz, jakie informacje potrzebujesz i co musisz obliczyć, żeby dowiedzieć się ile Twoi rodzice zapłacą za te klepki?
Metody:
Aktywizujące: rozmowa dydaktyczna z elementami metody problemowej, metoda czynnościowa Praktyczne: pokaz i obserwacja, ćwiczenia praktyczne
Programowe: praca z użyciem podręcznika programowego.
Na zajęciach lekcyjnych zastosowano elementy oceniania kształtującego.
Formy pracy: indywidualna, grupowa, z całą klasą
Środki dydaktyczne: podręcznik i zeszyt ćwiczeń dla klasy VI Matematyka 2001, modele rombów z kartonu dla nauczyciela, modele rombów dla uczniów, przyrządy geometryczne: linijka, ołówek, kolorowe kartoniki do gry PRAWDATAŁSZ, kolorowe kartoniki do „metody świateł”, kolorowa kreda, magnesy, klej.
PRZEBIEG ZAJĘĆ:
Faza wprowadzająca
I. Czynności organizacyjne:
sprawdzenie obecności, sprawdzenie pracy domowej
II. Część wstępna
1. Przypomnienie sposobu obliczania pola równo ległoboku
2. Zadanie pytania kluczowego: Wyobraź sobie, że podłogę w Twoim pokoju wykładamy drewnianymi klepkami w kształcie rombu. Jak sądzisz, jakie informacje potrzebujesz i co musisz obliczyć, żeby dowiedzieć się ile Twoi rodzice zapłacą za te klepki?
3. Zapoznanie uczniów z tematem lekcji oraz celami sformułowanymi w języku ucznia. Podanie nacobezu.
4. Rozdanie dwóch modeli rombów każdemu uczniowi.
Faza realizacyjna
1. Wyprowadzenie wzoru na pole rombu o danych przekątnych.
Uczniowie pod kierunkiem nauczyciela odkrywają sposób obliczania pola rombu o danych przekątnych.
■ Nauczyciel przypina do tablicy za pomocą magnesów dwa takie same modele rombów, jeden obok drugiego. Na polecenie nauczyciela uczniowie wykreślają kolorowym mazakiem na swoim modelu przekątne. Kolorują dwa trójkąty. Wskazany uczeń wykonuje to samo zadanie na modelu przymocowanym do tablicy.
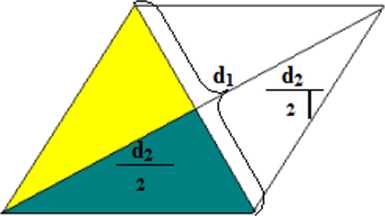
Opisujemy model:
di, d: - przekątne rombu
■ Na jakie figury przekątne podzieliły romb? (c ztery pr zystaj ące trójkąty prostokątne)
■ Uczniowie wklejają do zeszytu jeden z modeli rombu.
■ Następnie nauczyciel poleca uczniom przecięcie drugiego modelu wzdłuż przerywanych linii (odcinają dwa kolorowe trójkąty), a nauczyciel przecina model umieszczony na tablicy, po czym stawia przed uczniami następujący problem:
W jaki sposób należy ułożyć otrzymane części, aby zbudować z nich inny znany czworokąt?
Uczniowie manipulując figurami powinni ułożyć prostokąt, następnie wklejają go do zeszytu.
di
2
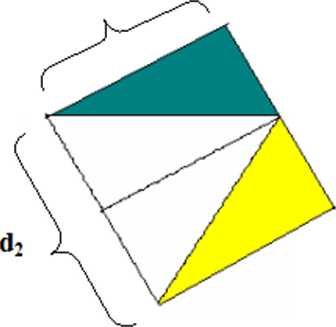
Nauczyciel prowadzi rozmowę dydaktyczną z uczniami:
Co można powiedzieć o polu rombu i otrzymanego prostokąta? (są równe)
- Jak oblicza się pole prostokąta? (mnożąc długość przez szerokość)
- Jaka jest długość naszego prostokąta, a jaka szerokość?
- Jak zapisać wzór na obliczanie pola prostokąta? Stosujemy oznaczenia z modelu.
Nauczyciel stawia przed uczniami kolejny problem:
W jaki sposób za pomocą oznaczeń literowych zapisać wzór na pole rombu?
Uczniowie powinni zauważyć, że pole prostokąta jest równe polu rombu, więc dla rombu prawdziwy jest ten sam wzór: d,-d,
P = —-— , gdzie dj, dj- diugości przekątnych rombu
Uczniowie zapisują wzór na pole rombu w zeszytach
2. Sformułowanie słowne wzoru.
Uczniowie formułują słowny opis sposobu obliczania pola rombu, używając języka matematycznego:
Pole rombu jest równe połowie iloczynu długości jego przekątnych.
Ważne jest, aby uczniowie nie tylko zapamiętali wzór, ale rozumieli go i potrafili wyjaśnić, co oznaczają litery w nim występujące.
r
3. Ćwiczenia utrwalające poznany sposób obliczania pola rombu.
Ćwiczenie: zmierz odpowiednie elementy (przekątne) i oblicz pole rombu wklejonego do zeszytu (praca samodzielna).
4. Ćwiczenia doskonalące umiejętności obliczania pola rombu, gdy dane są długości jego przekątnych - praca z podręcznikiem (w grupach 2 osobowych).
■ Zadanie 14 str. 59:
a) Oblicz pole kwadratu o przekątnych długości 4 cm.
b) Pole kwadratu wynosi 50 cm2. Jaka jest długość jego przekątnych?
■ Zadanie 16 str. 60
Pole rombu wynosi 49 cm2. Jedna z jego przekątnych ma długość 7 cm. Jaka jest długość drugiej przekątnej tego rombu?
Nauczyciel kontroluje pracę uczniów i w razie potrzeby wyjaśnia wątpliwości. (Zastosowanie „metody świateł”: jeśli uczeń ma problemy, pokazuje światło żółte lub czerwone)
5. Odpowiedź na pytanie kluczowe - wypowiedzi uczniów.
6. Wykorzystanie obliczania pola rombu w sytuacji rzeczywistej - rozwiązanie zadania 1 z karty pracy: Ile płytek w kształcie rombu potrzeba do wyłożenia podłogi w salonie państwa Trójkątnych? Jaki jest koszt tych płytek?
Faza podsumowująca
1. Podsumowanie - zdania podsumowujące:
■ Dziś nauczyłem się, że ...
■ Zaskoczyło mnie, że ....
■ Z dzisiejszej lekcji chciałbym (chciałabym) zapamiętać ...
2. Zadanie i omówienie pracy domowej.
■ Ćwiczenie Al-3, BI-3 strona 40-41 z zeszytu ćwiczeń (indywidualizacja pracy)
■ Dla chętnych: zadanie 2 z karty pracy
Notatki i dodatkowe ćwiczenia:
Dla uczniów, którzy wykonali poprawnie wszystkie zadania polecenie wymyślenia zadania, które wykorzystuje obliczanie pola rombu w praktyce.
KARTA PRACY UCZNIA
Pole rombu - ćwiczenia utrwalające

Zadanie 1.
Salon Państwa Trójkątnych ma kształt rombu (zdjęcie obok).
Wymiary salonu - rysunek pomocniczy:

8 m 6 m
<i,=
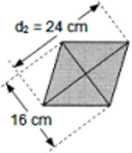
Podłoga w tym salonie zostanie wyłożona drewnianymi płytkami w kształcie rombu o wymiarach jak na rysunku:
a) Pomóż Państwu Trójkątnym obliczyć ile płytek potrzebują do wyłożenia tej podłogi.

b) Ile państwo Trójkątni zapłacą za płytki, jeśli paczka płytek, w której jest 10 sztuk, kosztuje 15 zł ?


Zadanie 2.
Pan Trójkątny zamówił drzwi z otworem w kształcie rombu o przekątnych
8dm i 6 dm. W to miejsce postanowił wbudować witraż, złożony z kolorowych szkiełek.
Jedna paczka takich szkiełek kosztuje 18,40 zł i wystarcza na położenie
wzoru na 240 cm2 powierzchni.
a) Ile takich paczek musi kupić pan Adam, żeby wykonać ten witraż?

b) Ile zapłaci pan Adam za szkiełka na witraż?
Wyszukiwarka
Podobne podstrony:
MATEMATYKA Scenariusz lekcji dla klasy VI Dział: Ułamki zwykłe TEMAT: Mnożenie ułamków i liczb
MATEMATYKA Scenariusz lekcji dla klasy VI TEMAT: Skala i plan. Powiązanie z wcześniejszą
I. Scenariusz lekcji dla klasy VI opracowany na podstawie książki J. Verne „80 dni dookoła świata” T
SWISSCONTRIBUTION 8. Scenariusz lekcji dla klasy IV-VI szkoły podstawowej i I klasy gimnazjum Temat:
13. Budowa czasopisma : scenariusz lekcji dla klasy IV / Bożena Hopa // Biblioteka w Szkole. - 2002,
71. Książki i katalogi : scenariusz lekcji dla klasy czwartej szkoły podstawowej /
7 117. Korzystamy z wydawnictw informacyjnych: scenariusz lekcji dla klasy IV / Vi
Scenariusz lekcji dla uczniów klasy VI wraz z załącznikami. Temat: Strach przed poezją. Czas: 2 godz
125. Spotkania ze sztuką - propozycja scenariusza zajęć dla klasy I z
9. Horodynska, Justyna : Propozycje lekcji dla klasy III / Justyna Horodynska
SWISSCONTRIBUTION 10. Scenariusz lekcji dla gimnazjów i szkół ponadgimnazjalnych Temat: Potrawy typu
97. W ŚWIECIE mitów : cykl lekcji dla klasy I / Ewa Banaś, Alicja Franczak// Język
LEKCJE ZE ŹRÓDŁAMI Konspekty i scenariusze lekcji dla nauczycieliWIEKXVI-XVIII iUvu»KhM. iiiUmc FftN
LEKCJE ZE ŹRÓDŁAMI Konspekty i scenariusze lekcji dla nauczycieliWIEK XVI-XVIII Vlł lUunirln n uAowr
więcej podobnych podstron