12795

Np.:

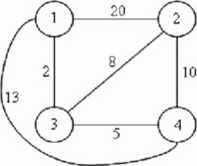
Dla jednego punktu startowego (3): ⁿ«v jot = (34,4,2) ę(fl) = 2 + 3+10+ 8 = 33 (bo wracamy do początku)

dla innego (4):

n.w_r»> =(4,3,1,2)    0(11) = 5+2+ 20+ 10 = 37

Def: Podzbiór rozwiązań N(.v)(c X,c D) [X - rozwiązania dopuszczalne, D -dziedzina problemu] nazywamy otoczeniem rozwiązania * jeżeli:

a) dla każdego ie X : 3N(x) (N(x) e 2' lub2")

b)    dla każdego x e X :.te N(x) (nie zawsze wymagany)

Def:    Rozwiązanie v° jest lokalnie optymalne (najlepsze w swoim otoczeniu), jeżeli

Q(x°) = mm{o(.v): xe -Y(.v⁰)}

ALGORYTMY POPRAW (algoiytmy optymalizacji lokalnej):

Klasyczny algoiytm optymalizacji lokalnej (wersja dla minimum - algorytm zstępujący)

1 wybierz rozwiązanie ; xx„

2.    spróbuj znaleźć x' takie, że Q(x^r) <Q(x) dla x'e ,V(.v)

3.    jeżeli istnieje x' to x := x' i powtarzamy krok 2, inaczej ,v° := x i stop

36 of 63