18624
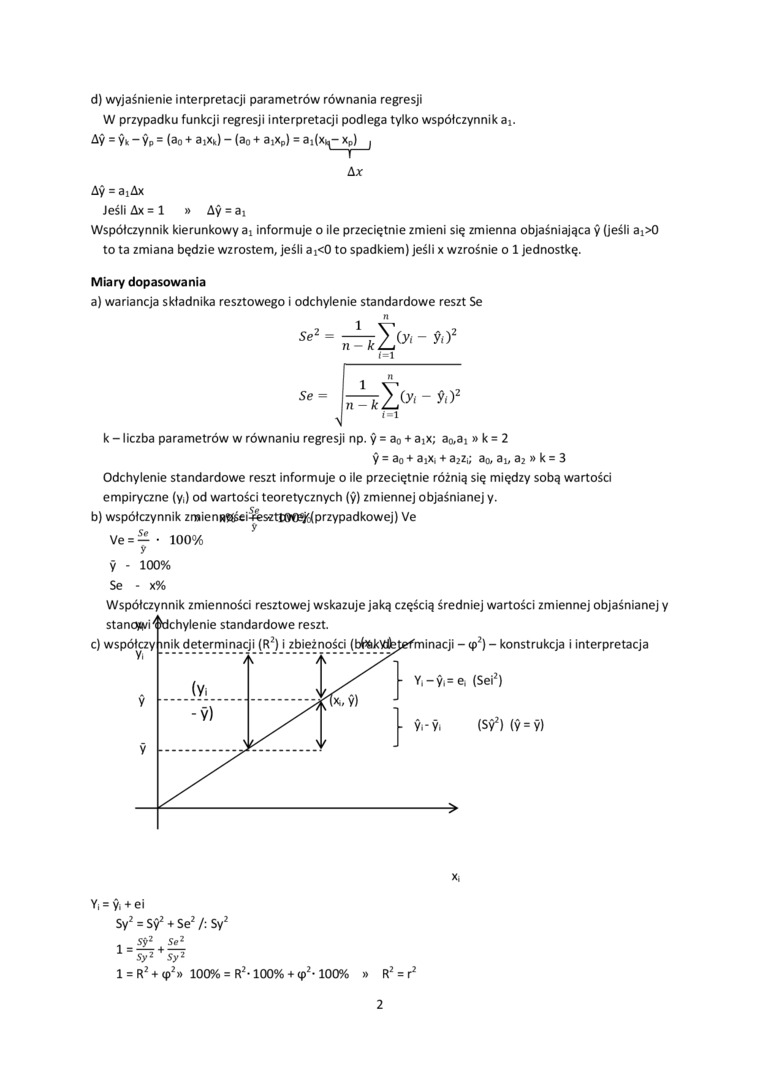
d) wyjaśnienie interpretacji parametrów równania regresji W przypadku funkcji regresji interpretacji podlega tylko współczynnik ai.
Ay = yk -yP = (a0 + apO - (a0 + aixp) = a,(x^-Xp)_J
A*
Ay = ajAx
Jeśli Ax = 1 » Ay = ai
Współczynnik kierunkowy ai informuje o ile przeciętnie zmieni się zmienna objaśniająca y (jeśli ai>0 to ta zmiana będzie wzrostem, jeśli ai<0 to spadkiem) jeśli x wzrośnie o 1 jednostkę.
Miary dopasowania
a) wariancja składnika resztowego i odchylenie standardowe reszt Se
Se2 = ;rhX<* - *>2
Se =
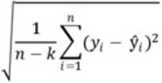
k - liczba parametrów w równaniu regresji np. y = a0 + aix; ao,ai » k = 2
y = a0 + apc + a2Zj; ao, ai, a2 » k = 3
Odchylenie standardowe reszt informuje o ile przeciętnie różnią się między sobą wartości empiryczne (yj) od wartości teoretycznych (y) zmiennej objaśnianej y. b) współczynnik zmienntóei-&wtflWEfc(przypadkowej)Ve
Se ^
Ve = — • 100%
9
y - 100%
Se - x%
Współczynnik zmienności resztowej wskazuje jaką częścią średniej wartości zmiennej objaśnianej y
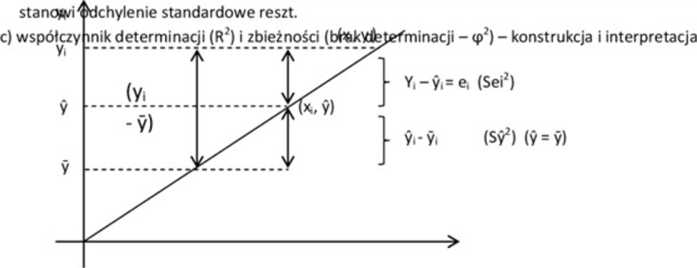
Yi = y, + ei
»
R2 = r2
2
Wyszukiwarka
Podobne podstrony:
statystyka skrypt�53 Do równania regresji dołącza się funkcję fk(x) dla której wartość F,* jest najw
img@31 (2) MNK- jest to metoda regresyjna, wykorzystywana do wyznaczania parametrów równania obiektu
statystyka skrypt�53 Do równania regresji dołącza się funkcję fk(x) dla której wartość F,* jest najw
Str 191 ny. Zatem również w przypadku małych zlewni można stosować obszarowe równanie regresji do ob
a —r- s(y) s(x) Interpretacja parametrów prostej regresji. a>0 jeśli „x" wzrośnie o 1
img283 Dlatego należałoby raczej określić równanie regresji wyższego stopnia, a następnie, po zbadan
Edward Laszyca, Renata Kuśmierek-Tomaszewska Tabela 2. Równania regresji i wielkość zmian średniej
Użycie zmiennych w postaci zumtaryzowanej pozwala w sposób bardzo jasny czytać równanie regresji: W„
Rzeczoznawca przyjmując wagi atrybutów, cenę maksymalną i minimalną, zdefiniował równanie regresji o
I Równania E-L większa liczba funkcji Przypadek szczególny
więcej podobnych podstron