20369

(45)

możemy pracę wykonaną w przedziale czasu od ^ do ^ wyrazie¹ jako

w_{t ti} = \r t dt

Moc

Szybkość wykonywania pracy przez daną siłę charakteryzuje moc. którą wyrażamy jako stosunek pracy do przedziału czasu ^ , w którym praca ta została wykouana.

_p=dw ₌ r_* ₌ f .

^    (4.6) Wzór (4.6)

pokazuje, że moc wyrazić można także jako iloczyn skalamy wektora siły i wektora prędkości ciała, do którego siła ta jest przyłożona.

Za jednostkę pracy przyjmuje się pracę jednostkowej siły przy przesunięciu równym jednostce długości i kącie pomiędzy wektorami siły i przesunięcia równym zeru.

Jednostką pracy w układzie SI jest jeden dzul (^    ^ ^ ^m)

Jednostką mocy jest taka moc. kiedy jednostkowa praca wykonana jest w jednostce czasu.

iw -i -

Jednostką mocy w układzie SI jest jeden wat (    ^s ).

Ł5iły_Łd.diQwmzę i dyttypanwiK

Powróćmy do przykładu narciarza. Przykład ten trakmjemy jako ilustrację całej klasy mchów odbywających się pod wpływem siły ciężkości.

Przy podchodzeniu w górę narciarz musi pokonać siłę grawitacji. Siła ta skierowana jest pionowo w dół i równa jest ciężarowi ciała. Praca tej siły przy mchu w górę ma znak ujemny, bowiem kąt pomiędzy kierunkiem siły i kierunkiem mchu jest rozwarty. Odwrotnie jest przy zjeżdzie w dół. Wtedy praca siły ciężkości ma znak dodatni.

Zależności te ilustruje Rys.4.3. przedstawiający schematycznie nasę narciarza, który wychodzi na górę o wysokości h z lewej strony wzniesienia (odcinek 1-2) przechodzi poziomy fragment trasy (odcinek 2-3). zjeżdża z prawej (odcinek 3-4). a następnie wraca do punktu wyjścia (odcmek 4-1).

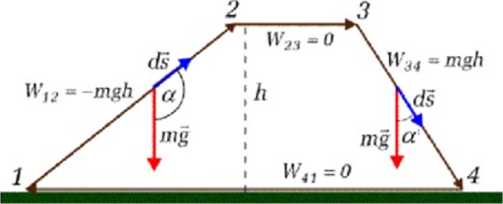
Rys.4.3. Schemat zamkniętego toru narciarza Podane sq wartości pracy wykonanej przez silę ciążenia na poszczególnych odcinkach toru.

Wektor siły ciężkości, pokazany kolorem czerwonym, ma kierunek pionowy, a jego wartość wynosi . Na pierwszym odcinku

tom zaznaczono elementarne przemieszczenie ^ oraz kąt. jaki twarzy ono z kierunkiem siły ciężkości, analogicznie do oznaczeii na Rys. 4.1. Wykorzystując wzór (4.1.) lub ogóbiiej (43) możemy wyznaczyć wartość pracy wykonanej przez siłę ciężkości na tym

odcinku Praca ta jest niezależna od kąta nachylenia stoku i wynosi    ^ 12 (^m S    (4.7)

Na odcuiku 3-4 wartość pracy będzie taka sama. ale znak będzie dodatni. W przypadku ruchu po poziomej części toru siła ciążenia nie wykonuje żadnej pracy, bowiem kierunek mchu jest prostopadły do kiemnku siły. Sumaryczna praca wyniesie więc.

W_t2*W₃₁ + W₃₄*W₄₁=-m' g h + 0*m g h*0~0    ₍₄₈₎

Otrzymaliśmy bardzo ważny wynik. Praca siły grawitacji po lorze zamkniętym jest równa zera Łatwo zauważyć, że wniosek ten pozostanie słuszny także i wtedy, kiedy tor będzie miał jakikolwiek, choćby bardzo skomplikowany, kształt. Zawsze bowiem możemy rozłożyć tor na sumę dowolnie małych odcinków prostoliniowych sprowadzając problem do rozpatrzonego powyżej.

Z faktu zerowania się pracy na terze zamkniętym wynika inny ważny wniosek. Praca potrzebna na przemieszenie ciała pod wpływem siły ciężkości pomiędzy dwoma dowobiymi punktami nie zależy od kształtu drogi a jedynie od położenia samych pimktów