2092

Definicja (całki potrójnej)

Jeśli dla każdego normalnego ciągu podziałów prostopadłościanu P, ciąg sum cząstkowych (S„)„,_N jest zbieżny do tej samej granicy właściwej, niezależnej od wyboru punktów At, to tę granicę nazywamy całką potrójną funkcji/w prostopadłościanie P i oznaczamy

p

JJJ/(x,y,.-)rfF:=limS„.

Uwaga    ^r

Jeśli funkcja ograniczona/ jest ciągła poza zbiorem miary zero (zbiór miary zero w R¹ to taki zbiór, który można pokryć skończoną liczbą prostopadłościanów, których siana objętości jest dowolnie mała (czyli mniejsza niż e )), to funkcja / jest całkowalna w prostopadłościanie P

Interpretacja geometryczna

f(x,y,:)= 1 => JJJr/F = V,\ - objętość prostopadłościanu P.

p

Interpelacja fizyczna

1 p(x, V,:Y gęstość objętościowa masy prostopadłościanu=>

=> JJJ P (x,y,:)tlV - masa prostopadłościanu P.

p

2. p(x,v,r)- gęstość objętościowa ładunku elektrycznego prostopadłościanuP =>

=> JJJ p(a:,.v, : )r/r - całkowity ladimek elektryczny gromadzony w P

p

Własności całki potr ójnej

Całka potrójna ma własności analogiczne jak całka podwójna (liniowość, addywność, ograniczoność)

Twierdzenie (całkowe o wartości średniej)

Jeśli

/- ciągła w prostopadłościanie P, to

3ce P f(c)-V_F =IUf(y,y,x)dV, gdzie V_r -objętość prostopadłościanu P P

Twierdzenie (o zamianie całki potr ójnej na cąlkę iterowaną)

Jeśli

P = [fl,ó]x[c,l/]x[p,<y],

/ e C(F), to

JJJ/(.r,y,.-)rfr = J

P    a

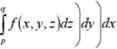
oraz prawdziwe są analogiczne wzoiy dla pozostałych pięciu całek iterowanych.

Oznaczenia

J J J/(r,y,;)rfr Wv dx = JrfvJrfrJ/(.r,.v,;)<t

b(dfq    \    ^ b d ą

dV = dxdydz

JJJ/(r,.v,r)dr' = jjjf(x,y,:)ix<fyd:

P    P

2