13473

Uwaga. Z definicji prawdopodobieństwa wynika, że dla każdego A 6 T. P(A) ^ 0. Ponadto, ponieważ .4 C 12. więc na mocy własności I prawdopodobieństwa mamy P(A) ^ P(12) - 1. Ostatecznie więc dla każdego zdarzenia /I

0 ^ P(A) ś 1.

4. Przykłady określania prawdopodobieństwa

4.1 Klasyczna definicja prawdopodobieństwa

Niech A będzie zbiorem skończonym. Wtedy A oznacza liczbę elementów zbioru .4.

Twierdzenie 1 Niech 12    {u>i,... .u;,,} będzie zbiorem skończonym. Jeśli wszystkie zdarzenia elementarne sąjed-

mikowo prawdopodobne, to znaczy

PM = £

dla każdego u€ 12. to dla dowolnego zdarzenia losowego A

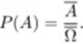
Klasyczną definicję prawdopodobieństwa podał w 1812 roku lepiące.

4.2 Przeliczalny zbiór zdarzeń elementarnych

Twierdzenie 2 Jeśli 12 —    ...} jest zbiorem przeliczalnym, to dla dowolnego zdarzenia losowego A

P(A)= y. ^pM-

w.e/t}

4.3 (Geometryczna definicja prawdopodobieństwa

Uwaga. Jeśli A C R". to |zl| jest miarą Lcbcsguc‘a zbioru A. to znaczy: jeśli n a* 1, to |-4| - długość; jeśli n = 2. to |z4| - pole; jeśli u - 3. to |zl| - objętość.

Twierdzenie 3 Niech 12 C R" , n ^ 1, gdzie 12 ma skończoną i niezerową n-wymiarowq miarę Lebesgue 'a. Wówczas dla każdego zdarzenia losowego A

PI A) - B

^P{A) ~ |S2|

2