17737

2

zbiór punktów styczności jest wartością funkcji korespondencji dla wektora p. Jeśli p wskazuje „do wewnątrz” Y, to oznacza, że musimy prostą H zacząć przesuwać w drugą stronę, tak, by zbiór Y znalazł się po przeciwnej stronie tej prostej. Jeśli nie uda się nam otrzymać sytuacji takiej, jak na rysunku 1, to korespondencja podaży dla danego wektora nie jest określona, czyli wektor p nie należy do dziedziny korespondencji tj.

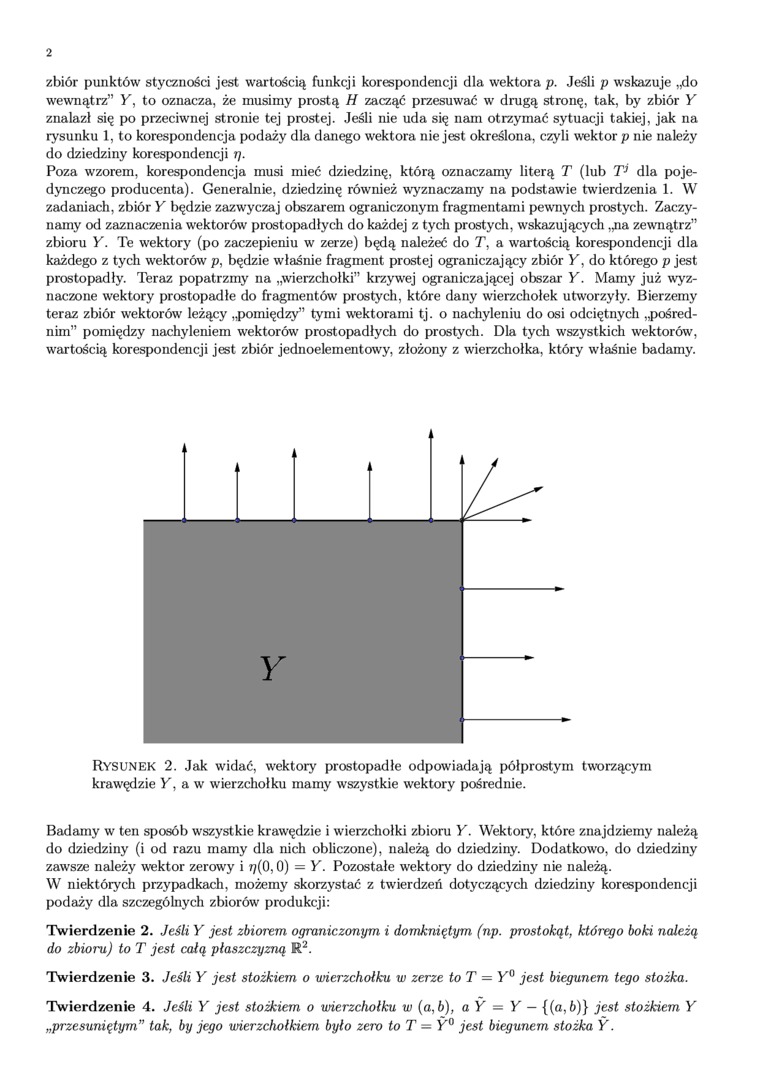
Poza wzorem, korespondencja musi mieć dziedzinę, którą oznaczamy literą T (lub dla pojedynczego producenta). Generalnie, dziedzinę również wyznaczamy na podstawie twierdzenia 1. W zadaniach, zbiór Y będzie zazwyczaj obszarem ograniczonym fragmentami pewnych prostych. Zaczynamy od zaznaczenia wektorów prostopadłych do każdej z tych prostych, wskazujących „na zewnątrz” zbioru Y. Te wektory (po zaczepieniu w zerze) będą należeć do T, a wartością korespondencji dla każdego z tych wektorów p, będzie właśnie fragment prostej ograniczający zbiór Y, do którego p jest prostopadły. Teraz popatrzmy na „wierzchołki” krzywej ograniczającej obszar Y. Mamy już wyznaczone wektory prostopadłe do fragmentów prostych, które dany wierzchołek utworzyły. Bierzemy teraz zbiór wektorów leżący „pomiędzy” tymi wektorami tj. o nachyleniu do osi odciętnych „pośrednim” pomiędzy nachyleniem wektorów prostopadłych do prostych. Dla tych wszystkich wektorów, wartością korespondencji jest zbiór jednoelementowy, złożony z wierzchołka, który właśnie badamy.

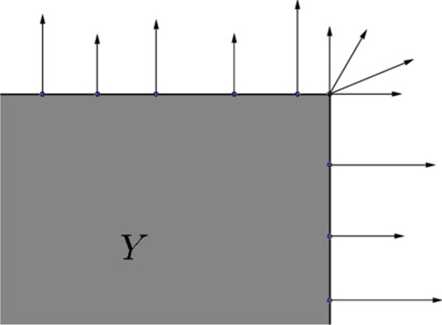
Rysunek 2. Jak widać, wektory prostopadłe odpowiadają półprostym tworzącym kraw^rędzie Y, a w wierzchołku mamy wszystkie wektory pośrednie.

Badamy w ten sposób wszystkie krawędzie i wierzchołki zbioru Y. Wektory, które znajdziemy należą do dziedziny (i od razu mamy dla nich obliczone), należą do dziedziny. Dodatkowo, do dziedziny zawsze należy wektor zerowy i 77(0,0) = Y. Pozostałe wektory do dziedziny nie należą.

W niektórych przypadkach, możemy skorzystać z twierdzeń dotyczących dziedziny korespondencji podaży dla szczególnych zbiorów produkcji:

Twierdzenie 2. Jeśli Y jest zbiorem ograniczonym i domkniętym (np. prostokąt, którego boki należą do zbioru) to T jest całą płaszczyzną R².

Twierdzenie 3. Jeśli Y jest stożkiem o wierzchołku w zerze toT = Y° jest biegunem tego stożka.

Twierdzenie 4. Jeśli Y jest stożkiem o wierzchołku w (a,6), a Y = Y — {(a, 6)} jest stożkiem Y „przesuniętym” tak, by jego wierzchołkiem było zero to T =Y° jest biegunem stożka Y.