414223707

Efektem wykonanych obliczeń jest zbiór punktów o współrzędnych (y,-,Xj). Wartość oczekiwaną i należy estymować za pomocą regresji liniowej opisanej przez równanie prostej w postaci kierunkowej; poszukiwana wartość modułu Kirchoffa G równa jest wartości współczynnika kierunkowego b. Postać ogólna równania:

y = a + bx    (5)

gdzie, na potrzeby niniejszego ćwiczenia:

y - wartość oczekiwana naprężenia stycznego t [MPa], b - moduł sprężystości poprzecznej G (moduł Kirchoffa) [MPa], x - odkształcenie postaciowe y.

W celu wyznaczenia wartości a oraz b równania (5) posłużyć należy się zależnościami (5.23) i (5.24) [1], przy czym w powyższych wzorach za y przyjąć należy naprężenie styczne x.

Tą część ćwiczenia należy podsumować przez wygenerowanie wykresu x (y). Pierwszym krokiem jest naniesienie punktów wykorzystanych do analizy regresji (pierwsza seria danych). W kolejnym kroku generujemy prostą w oparciu o opracowane równanie kierunkowe (druga seria danych). Postać takiego wykresu przedstawiona jest na rysunku 3. Aktualna postać wykresu poddana zostanie dalszej modyfikacji w miarę opracowywania sprawozdania.

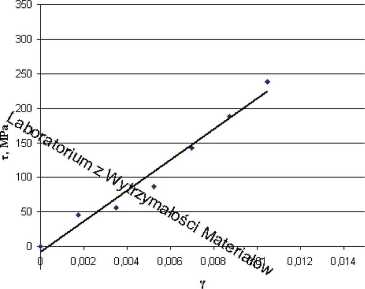
Rys. 3. Liniowa zależność naprężeń stycznych x od odkształceń postaciowych y

Liniowa zależność która została opracowana a następnie przedstawiona na rysunku 3 ma swój początek poniżej punktu o współrzędnych (0,0). Analiza takich wyników powinna mieć miejsce we wnioskach do sprawozdania.

5