36672

I. WSTĘP TEORETYCZNY

Podczas ruchu obrotowego wszystkie punkty ciała zataczają okręgi prostopadłe do osi obrotu wyznaczonej przez środki tych okręgów. Przy obrocie bryły sztywnej promienie wodzące oraz wszystkie inne punkty zataczają jednakowy kąt w tym samym czasie t. Punkty te mają tą samą

prędkość kątową ^0}. Jej kierunek wyznaczony jest przez oś obrotu. Jeśli w dowolnych, równych przedziałach czasu bryła obraca się o jednakowy kąt . wówczas taki ruch nazywamy ruchem obrotowym jednostajnym. W ruchu

ta -u -const.

tym prędkość kątowa jest stała:    ^    (1)

Ruch obrotowy bryły, podczas którego prędkość kątowa zmienia się nazywamy zmiennym. W ruchu tym przyspieszenia kątowe wszystkich punktów w dowolnej chwili są sobie równe. Jeżeli przyspieszenie kątowe jest wielkością stałą, wówczas ruch nazywamy ruchem obrotowym jednostajnie zmiennym.

Energia kinetyczna ^E» ciała sztywnego obracającego się wokół osi jest równa sumie energii kinetycznych poszczególnych jego elementów czyli:

E,    + |Am₂vś+ .+ |Am,rf

przy czym v = cd -r więc wzór przyjmuje postać :

E_r = £(Am_tr² -+ Am_ar² ■+......-tAm^r²) (D²

E,=|l<o^J    p)

Momentem bezwładności bryły nazywamy sumę iloczynów mas poszczególnych jej elementów i ich kwadratów odległości od osi obrotu :

I = Am_ttf + Am^+ +Am„ r_n² [kg m^{1 2} ]    (3)

Prarwa dynamiki

Przyspieszenie kątowe obracającej się bryły jest wprost proporcjonalne do momentu siły (względem osi obrotu) wywołującego ten ruch, a odwrotnie proporcjonalne do momentu bezwładności bryły (liczonego również względem osi obrotu)

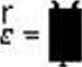
(5

1

I

Jeżeli na bryłę nie działa zewnętrzny moment sił M lub suma momentów sił jest równa zeru, wówczas przyspieszenie kątowe ^£ jest również równe zeru P³⁰ *

Zasada zachowania momentu pędu

Jeżeli wypadkowy moment sił zewnętrznych działających na ciało jest równy zeru. wówczas jego moment pędu ma wartość stałą (zostaje zachowany).

2

I = const.