9729

Po podzieleniu siły przez masę otrzymuje sę przyspieszenie z jakim jedno masa (o) porusza się w polu drugiej (M)

^S~~°S

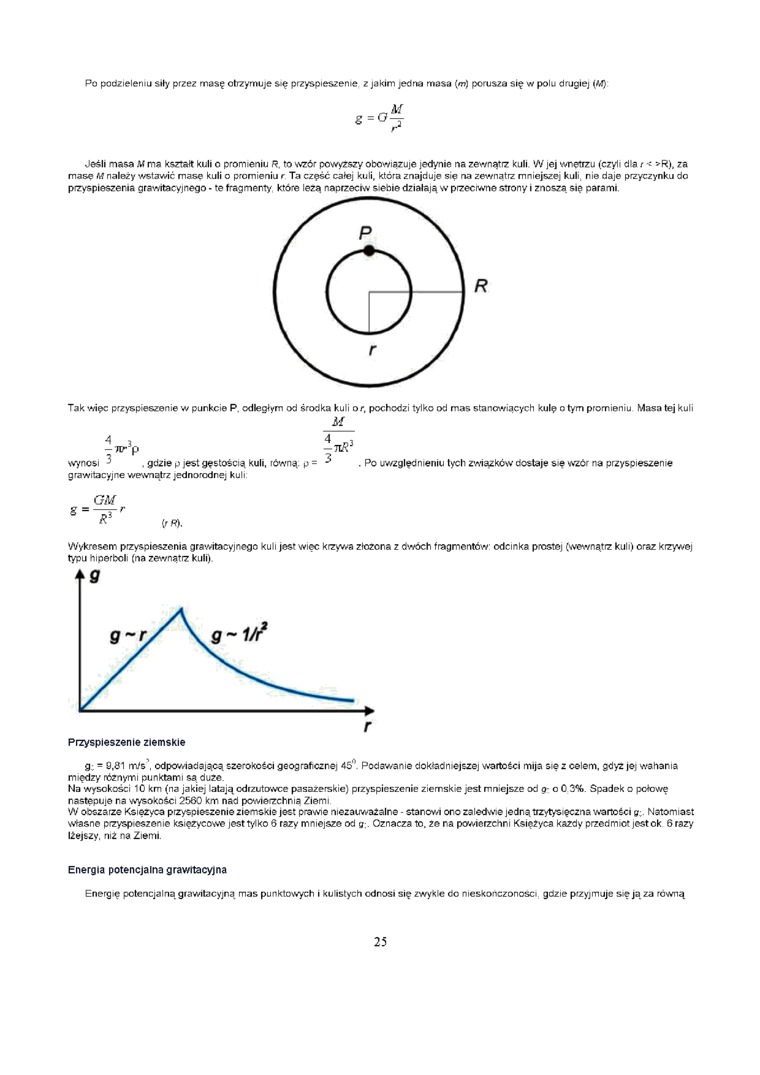
Jeśli masa M ma kształt kuli o promieniu R. to wzór powyższy obowiązuje jedynie na zewnątrz kuli W jej wnętrzu (czyli dla t < »R), za masę M należy wstawić masę kuli o promieniu r Ta część całej kuli, która znajduje się na zewnątrz mniejszej kuli nie daje przyczynku do przyspieszenia grawitacyjnego • te fragmenty które lezą naprzecrw siebie działają w przeciwne strony i znoszą się parami

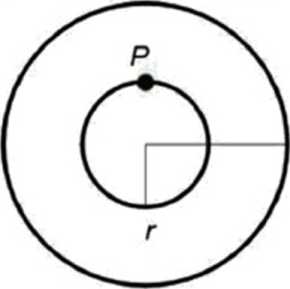
Tak więc przyspieszenie w punkcie P odległym od środka kuli or, pochodzi tylko od mas stanowiących kulę o tym promieniu Masa tej kuli

M

-tiR³

wynosi ³    . gdzie p jest gęstością kuli, równą: p = ^ .Po uwzględnieniu tych związków dostaje sie wzór na przyspieszenie

grawitacyjne wewnątrz jednorodnej kuli

GM

^s~F^r

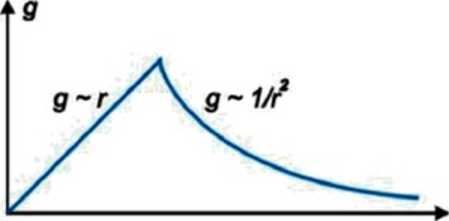
Wykresem przyspieszenia grawitacyjnego kuli jost więc krzywa złozena z dwóch fragmentów odcinka prostoj (wewnątrz kuli) oraz krzywej typu hiperboli (na zewnątrz kuli)

r

Przyspieszenie ziemskie

g. = 9.81 m/s', odpowiadającą sze-okośo geograficznej 45° Podawanie dokładniejszej wartości mija się z celem, gdyż jej wahania między różnymi punktami sa duże.

Na -wysokości 10 km (na jakiej latają cdrzutowce pasażerskie) przyspieszenie ziemskie jest mniejsze od o o 0 3%. Spadek o połowę następuje na wysokości 2560 km nad powierzchnia Ziemi

W obszarze Księżyca przyspieszenie ziemskie jest prawie niezauważalne - stanowi ono zaledwie jedną trzytysięczna wartości sr;. Natomiast wtasne przyspeszome księżycowe jest tytko 6 razy mniejszo od g_:. Oznacza to. zo na powierzchni Księżyca każdy przedmiot jest ok 6 razy lżejszy, mź na Ziemi.

Energia potencjalna grawitacyjna

Energię potencjalną grawitacyjną mas punktowych i kulistych odnosi się zwykle do nieskończoności gdzie przyjmuje sę ją za równą

25