Kolendowicz06

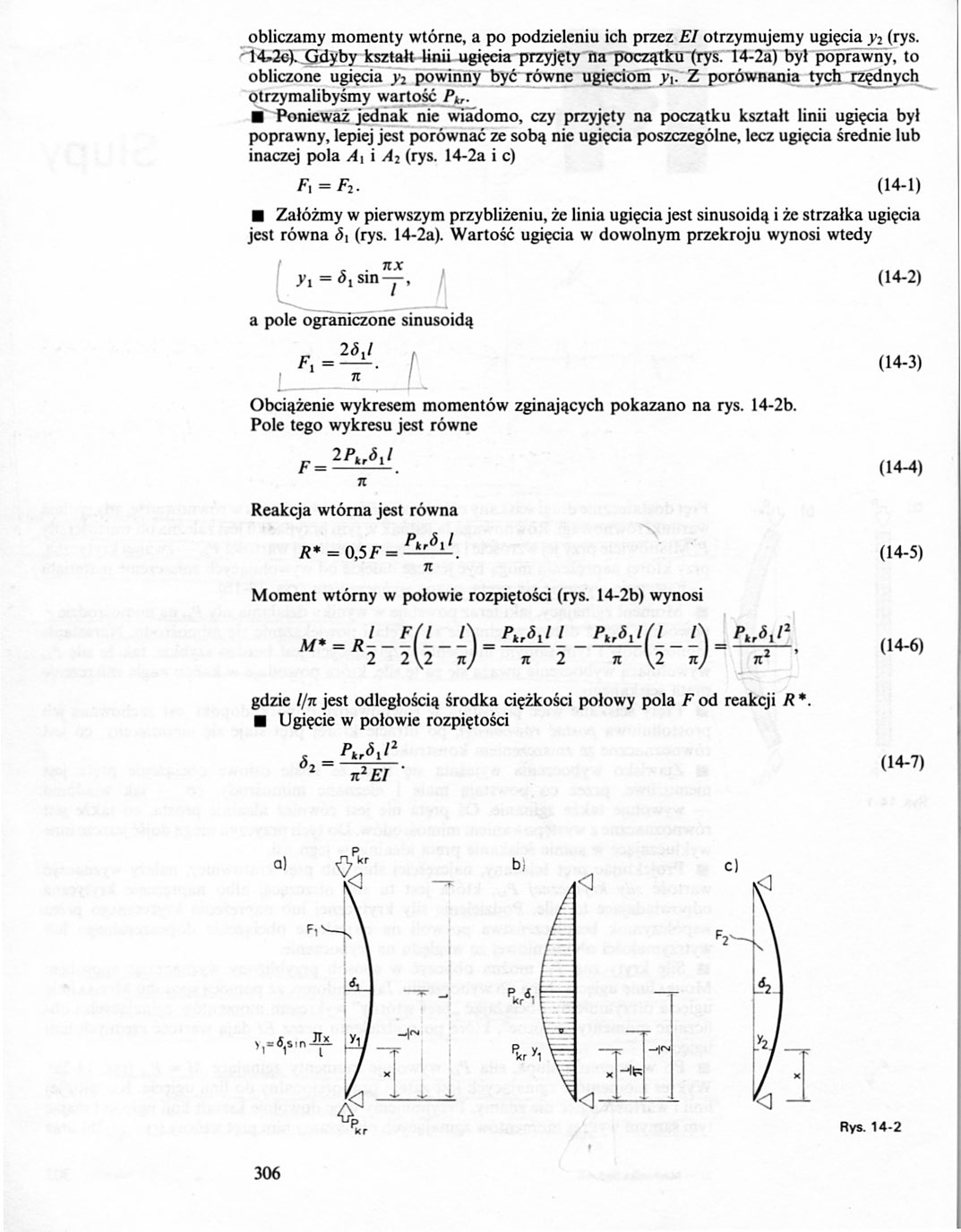
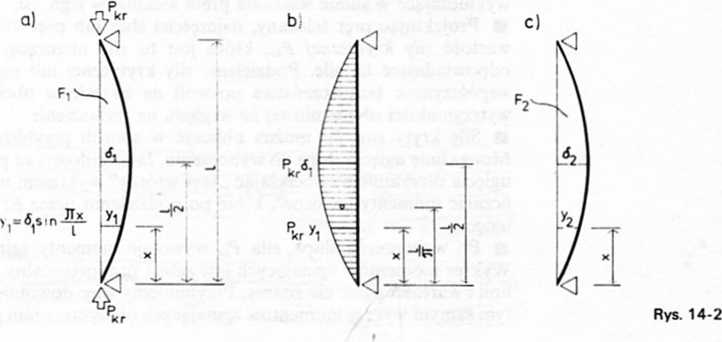
obliczamy momenty wtórne, a po podzieleniu ich przez El otrzymujemy ugięcia y₂ (rys. ' 14*2c). Gdyby kształt linii ugięcia przyjęty na początku (rys. 14-2a) był poprawny, to obliczone ugięcia y₂ powinny być równe ugięciom y_t: Z porównania tych rzędnych otrzymalibyśmy wartość P_kr.

■    Ponieważ jednak nie wiadomo, czy przyjęty na początku kształt linii ugięcia był poprawny, lepiej jest porównać ze sobą nie ugięcia poszczególne, lecz ugięcia średnie lub inaczej pola A, i A₂ (rys. 14-2a i c)

fj=f₂.    (14-1)

■    Załóżmy w pierwszym przybliżeniu, że linia ugięcia jest sinusoidą i że strzałka ugięcia jest równa <5| (rys. 14-2a). Wartość ugięcia w dowolnym przekroju wynosi wtedy

(14-2)

(14-3)

(14-4)

(14-5)

(14-6)

(14-7)

_s • ^nx y ,=<5iSin—,

a pole ograniczone sinusoidą

*-£!. f

1_

Obciążenie wykresem momentów zginających pokazano na rys. 14-2b. Pole tego wykresu jest równe

F-”sdli.

n

Reakcja wtórna jest równa

R* = 0,5F =^i-^/.

n

Moment wtórny w połowie rozpiętości (rys. 14-2b) wynosi

... J F(l l\ P_krS_tll PMfl l\ P_łr<5,/² M =R2-2\2-n) = ^T2--n \2 ~ n) ----

gdzie l/n jest odległością środka ciężkości połowy pola F od reakcji R *. ■ Ugięcie w połowie rozpiętości

ó₂ =

n² El

306