80168 skanuj0037 (2)

Arii = mmax
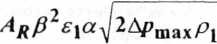
(9)
a po podzieleniu obu stron przez strumień maksymalny funkcja obliczeniowa przyjmie postać:
Arii
mat
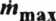
(10)
Obliczenia projektowe powinny być wykonywane w następującej kolejności:
1) w pierwszym kroku projektowym należy z katalogu przetworników pomiarowych dobrać
wstępnie stosowny przetwornik np. typu APQ lub EPA oraz maksymalny zakres ciśnienia
różnicowego Apmax, poczynając od wartości najmniejszej dla wybranego typu, gdyż
gwarantuje ona najmniejsza stratę ciśnienia,
2) obliczyć wartość i znak funkcji ni dla dolnej granicy przedziału przewężenia p = 0,2,
3) obliczyć wartość i znak funkcji ni dla górnej granicy przedziału przewężenia P = 0,75,
4) jeśli funkcja p ma ten sam znak w obu wynikach i jej wartość jest różna od zera, należy przyjąć przetwornik o większym zakresie, gdyż dja wersji poprzedniej przepływomierz jest nierealizowalny. Dla nowego zakresu przetwornika należy powtórzyć obliczenia z punktów 2 i 3,
5) różne znaki funkcji p w obu wynikach oznaczają, że istnieje rozwiązanie problemu, dla przyjętego przetwornika. Należy obecnie droga iteracji znaleźć taką wartość p, która spełnia nierówność:
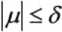
(U)
gdzie 5 - założona dokładność obliczeń, np. 8 = 0,001
Przewężenie kryzy p, w kolejnych iteracjach, należy przyjmować z przedziału 0,2 < p < 0,75. Wyznaczona średnica kryzy d oraz przewężenie p powinny spełniać następujące ograniczenia:
d>dmin=n,5mm oraz Sp(j])<Spma x (12)
Równanie charakterystyki przepływowej zaprojektowanej kryzy ma postać:
(13)
th = Kfę-^fAp
w którym czterech różnych elementów zainstalowanych na rurociągu przed zwężka. Dla wartości bez nawiasu niepewność dodatkowa współczynnika przepływu ma wartość zerowa, natomiast dla wartości w nawiasach niepewność dodatkowa ma wartość 0,5 %.
Chropowatość powierzchni odcinka pomiarowego przed zwężka nie powinna przekraczać wartości podanych w tablicy 2.
Tablica 2. Górne granice chropowatości względnej
|
p |
>0.3 |
0,32 |
0,36 |
0.38 |
0.4 |
0,45 |
0.5 |
0.6 |
0.75 |
|
104 k/D |
25 |
18.1 |
10.0 |
8.3 |
7.1 |
5.6 |
4.9 |
4.2 |
4.0 |
Wartość k chropowatości równoważnej, wyrażonej w jednostkach długości zależy od wielu czynników takich jak: wysokość nierówności, rozkład, kąty i inne parametry geometryczne elementów chropowatości ścianki rurociągu. Przybliżone wartości k dla różnych materiałów podane są w literaturze [2], [3]. Przykładowo:
dla nowej rury stalowej przeciąganej na zimno bez szwu k < 0,03mm, a dla rury stalowej zardzewiałej k ~ 0.25 mm.
2.4. Charakterystyka przepływowa
Do opisu charakterystyki przepływowej zwężek pomiarowych w literaturze [3], [4] .stosowana jest zależność wynikająca z bilansu energii strugi:
m = Azasx ^jlAppi <d
gdzie: Az - pole powierzchni przepływowej otworu zwężki, m2; m - strumień masy, kg/s; a - liczba przepływu;
Bi - liczba ekspansji dla parametrów płynu przed zwężką;
Ap - ciśnienie różnicowe, Pa;
pi - gęstość płynu dla parametrów przed zwężką, kg/m3.
Liczba przepływu jest funkcją liczby Reynoidsa Reo dla parametrów płynu w rurociągu przed zwężką oraz zredukowanego pola powierzchni przepływowej otworu zwężki m = (d/D)2, zwanego jej modułem. W nowej normie [3] w miejsce liczby przepływu a i modułu m wprowadzono współczynnik przepływu C i przewężenie zwężki p. Związki funkcyjne między tymi wielkościami są następujące:
C
(a)
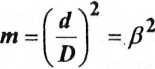
(b)
Wyszukiwarka
Podobne podstrony:
1.4. WODA GRUNTOWA stąd po podzieleniu obu stron przez ik zastępczy współczynnik k przy filtracji po
100?68 W wyniku porównania równania otrzymuje się: Po pomnożeniu obu stron przez pole pierścienia mi
skanuj0008 (309) 270 Ćwiczenia laboratoryjne z fizyki o — j . o~k dMi 2 ° (34.3) stąd po zlogarytmow
I 270 Ćwiczenia laboratoryjne z fizyki/. 2 /„• (34.3) stąd po zlogarytmowaniu obu stron
DSC07315 52 Wielomiany Po pomnożeniu obu stron powyższej równości przez mianownik funkcji wymiernej
82521 P1020488 md(v — =F o dr dt<ttyi Po scałkowaniu obu stron tego równania otrzymamy: mv2 •-2mv
I 270 Ćwiczenia laboratoryjne z fizyki/. 2 /„• (34.3) stąd po zlogarytmowaniu obu stron
I 270 Ćwiczenia laboratoryjne z fizyki/. 2 /„• (34.3) stąd po zlogarytmowaniu obu stron
DSC05205 a po podzieleniu obu równań stronami otrzymujemy: (2.61)n, _ Aba Ponieważ obydwie ciecze wy
353 (9) 1*0 podstawieniu tego wyrażenia do licznika i podzieleniu obu stron równania przez 2 otrzymu
I 270 Ćwiczenia laboratoryjne z fizyki/. 2 /„• (34.3) stąd po zlogarytmowaniu obu stron
Podstawiając równanie (**) do (*) otrzymamy:p*-dk+ -r(]H=p* a po wymnożeniu obydwóch stron przez
więcej podobnych podstron