4130649990

1.4. WODA GRUNTOWA

stąd po podzieleniu obu stron przez ik zastępczy współczynnik k przy filtracji poprzecznej wynosi

(1.32)

(1.33)

E(1 /ki)Li

Dla określenia filtracji w przestrzeni 3D używamy pojęcia gradientu przestrzennego naporu h, czyli

(d /dxi)

Vi =    lub v = -k^ = -fcV/i =-k{ (d /dx₂) \ h

('9 /«■*) _

Warunek zachowania masy (zakładamy ośrodek gruntowy jest nasycony i że gęstość wody nie zmienia się) oznacza, że w sześcianiku dzida^dżą nie może wody przypywac ani ubywać, czyli    = 0

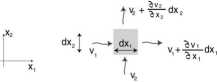
Rys. 1.11: Warunek zachowania masy

z czego otrzymujemy

Vv = 0    (1.34)

skąd podstawiając prawo Darcy uzyskamy równanie

S>i|=»    i¹'³⁵)

Ostatnia postać nazywa się równaniem Laplace’a pola o potencjale h. Linie ekwipotencjalne to takie na których napór jest stały h = const. Prostopadle do nich leżą linie prądu. Są one styczne do wektora prędkości v = —k(dh/dx).

Konstruowania siatek hydraulicznych:

•    Narysować skrajne linie prądu wzdłuż brzegów nieprzepuszczalnych || do linii prądu i _L do linie ekwipotenc-jalnej.

•    Narysować linie kontaktu z wodą wolną jako skrajne linie ekwipotencjalne hpocz i hkoniec odpowiadające początkowj i końcowej wysokości naporu

•    Podzielić różnicę między hpo_CZ i hkoniec na np. n_OCzek = 10 równych części i narysować przypuszczalne pośrednie Unie ekwipotencjalne pamiętając o prostopadłości do skrajnych linii prądu.

•    wrysować pośrednie linie prądu prostopadle do linii ekwipotencjalnych. Liczbę linii prądu dobrać tak aby powstała siatka filtracji tworzyła ± kwadratowe oczka.

•    sukcesywnie poprawiać kształt siatki (prostopadłość linii i kwadratowość oczek) korygując jeśU trzeba liczbę kanałów lub oczek w kanale.

Jako pojedynczy kanał definiujemy obszar między dwoma sąsiednimi liniami prądu. Przez każde oczko jednego kanału filtruje ta sama ilość wody czfi v = const. Wydatek z jednego kanału to ilość wody filtrująca przez i-te oczko sieci o szerokości 6,

(1.36)

(1.37)

Qi = Vibi = const

= const

tyle samo wody przepłynie przez każde oczko kanału w jedn. czasu. Zakładamy że oczka są ± kwadratowe, tj. b Rs l gdzie b to wymiar poprzeczny.