109547

Równia pochyla

Rozkład sil na równi z uwzględnieniem siły tarcia

Równię pochylą otrzymamy, gdy nachylimy plaska powierzchnię (np. deskę) do poziomu pod pewnym kątem. Wtedy siła ciężkości rozkłada się na dwie składowe - prostopadłą do równi silę nacisku i równoległą silę zsuwającą.

Siła ciężkości P\=mg rozkłada się na dwie siły składowe:

*    równoległą do powierzchni równi silę zsuwającą równą sile ciężkości pomnożonej przez sinus kąta nachylenia ^1 =PsiflOf .ostatecznie

Fi = mg sin a .

*    prostopadłą do powierzchni równi silę nacisku, którą otrzymujemy mnożąc silę ciężkości przez cosinus katą nachylenia: ^2 = mg cos ar

Prócz tego mamy:

•    silę reakcji podłoża (patrz III zasada dynamiki Newtona) N;

•    silę tarcia (jak pamiętamy jest to siła nacisku pomnożona przez współczynnik tarcia): ^ ⁼ M i ostatecznie

T = mg fi cos a

Przyspieszenie na równi pochyłej

to tak: Fi = T + F_b Dalej mi? sin a - mg (i cos a + ma _apo

przekształceniach otrzymujemy wzór na przyspieszenie:

Ponieważ ciało na równi porusza się ruchem jednostajnie przyspieszonym, siły powodujące nich (siła zsuwająca) równe są silom hamującym (siła tar cia) i sile bezwładności. Zapisujemy

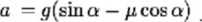
W powyższych:

a - kąt nachylenia równi do poziomu

T - siła tarcia

Fb - siła bezwładności

# - średnie przyspieszenie grawitacyjne Ziemi m - masa ciała p - współczynnik tarcia