new 41 (2)

86 4. Rozkład sił na gwincie

Jeśli szerokość powierzchni styku (S—d₀)/2 jest mała w porównaniu ze średnim promieniem styku, to dla uproszczenia obliczeń można przyjmować promień tarcia równy średniemu promieniowi styku

r_t =

(4.15)

Całkowity moment z uwzględnieniem oporów tarcia łba śruby lub nakrętki o powierzchnię elementu łączonego wyraża wzór

(4.16)

M_c=M_t + M_s.

W niesamohamownych połączeniach śrubowych istnieje możliwość zamiany ruchu obrotowego na ruch postępowy, jak również zamiany ruchu postępowego na obrotowy.

Przy zamianie ruchu obrotowego na postępowy, praca włożona na drodze jednego pełnego obrotu jest równa L_w — 2nM_s, zaś praca uzyskana L_u=QP_h, gdzie P_h=nd_s tgy.

Z powyższej zależności oraz z równania (4.12) otrzymujemy wzór określający sprawność gwintu

_ L_u _ QPh _ Qnd,tgy    _ tgy_    „

^V L_w 2 iM,' 2n 0,5d,Qtg(y+_e') tg(y+_e') ^-    1 * ’

Przebieg zmiany sprawności w zależności od kąta wzniosu gwintu y, dla gwintu trapezowego symetrycznego o kącie boku a_r=15° przy różnych współczynnikach tarcia /u przedstawiono na rys. 5.1.

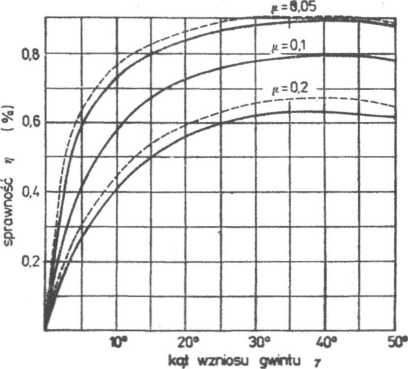
Rys. 5.1. Sprawność gwintu

gwnt o zarysie trapezowym (a, = 3*

gwint o zarysie trójkątnym U, = 30^ai