new 39

82 4. Rozkład sił na gwincie

Rozkład obciążeń przy podnoszeniu ciężaru Q na śrubie (przesuwaniu w górę ciężaru po równi pochyłej) przedstawia rys. 4.1c. Śruba (ciężar Q) przemieszcza się po powierzchni gwintu nakrętki (równi) pochylonej pod

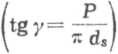
kątem wzniosu gwintu y

pod działaniem siły obwodowej H

leżącej w płaszczyźnie prostopadłej do osi gwintu. Siła H na ramieniu ~ wynika bowiem z momentu jaki jest przykładany na pokrętle śruby:

M_S=H-f-.    (4.1)

Przemieszczeniu śruby przeciwstawia się siła tarcia

T—juN = N tgo,    (4.2)

gdzie /z=tgo jest współczynnikiem tarcia    między śrubą i nakrętką,

a q — kątem tarcia.

Wypadkowa siła oddziaływania nakrętki na śrubę R~ ]/ N²+T²= = N y l-f^u² tworzy z siłą Q kąt y + g (rys. 4.Id), stąd

H=Q tg(y+e).    (4.3)

Na podstawie zależności (4.1) moment skręcający jest równy

M_s=0,bd_sQ tg(y+g).    (4.4)

4.2. Rozkład sił przy opuszczaniu ciężaru na śrubie

z gwintem prostokątnym

Zależnie od relacji jaka zachodzi między kątem wzniosu gwintu y i kątem tarcia q rozróżnia się dwa przypadki rozkładu obciążeń.

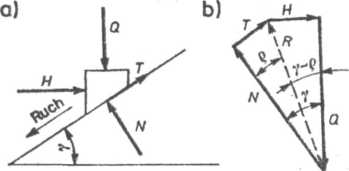
Rys. 4.2. Rozkład sił działających na śrubę z gwintem prostokątnym niesa-

mohamownym przy opuszczaniu ciężaru: a) rozkład sił na równi pochyłej, b) zamknięty wielobok sił

H

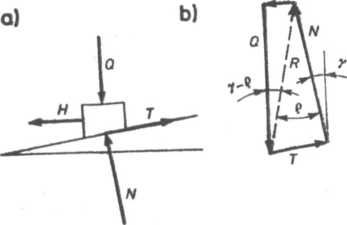
Rys. 4.3. Rozkład sił działających na śrubę z gwintem prostokątnym samo-hamownym przy opuszczaniu ciężaru: a) rozkład sił na równi pochyłej, b) zamknięty wielobok sił

Gdy y > g, rozkład sił w połączeniu przedstawia rys. 4.2. W tym przypadku dla zrównoważenia układu należy przyłożyć siłę H, gdyż siła tarcia T przeciwstawiająca się ruchowi nie wystarcza aby utrzymać zsuwający się po równi pochyłej ciężar Q. Układ taki nazywamy niesamo-hamownym. Wypadkowa siła oddziaływania nakrętki (równi) na śrubę (ciężar) R tworzy z siłą Q kąt y—g (rys. 4.2). Stąd siłę poziomą H wyznaczyć można ze wzoru

H=Q tg(r-e).    (4.5)

Moment obrotowy M_s, jaki trzeba przyłożyć aby powstrzymać samorzutnie wkręcającą się śrubę jest równy:

M_s=0,5d_sQ tg(y—g).    (4.6)

Gdy y<g, rozkład sił w połączeniu będzie taki jak na rys. 4.3. W tym przypadku siła tarcia T jest dostatecznie duża, aby nie pozwolić na zsunięcie się ciężaru Q, a dla zsunięcia ciężaru trzeba przyłożyć dodatkowo siłę H. Układ taki nazywamy samohamownym. Z warunków równowagi (zamknięty wielobok sił na rys. 4.3), wynika:

H=Qtg(g-y).    (4.7)

Jeśli przez analogię do poprzednio rozpatrywanego przypadku zmienimy zwrot wektora siły H, otrzymamy H=Q tg(y—o), czyli wzór (4.5). Wartość siły H jest wtedy oczywiście ujemna. W tym przypadku obliczony ze wzoru (4.6) moment obrotowy M_s trzeba przyłożyć, aby opuścić na śrubie ciężar Q.

4.3. Rozkład sił w połączeniu śrubowym z gwintem

o dowolnym zarysie

W gwintach, w których roboczy kąt boku gwintu a_r =£ 0, rozkład obciążeń jest inny niż w gwincie o zarysie prostokątnym. W gwintach tych bowiem siła normalna N (rys. 4.4 a, b) odchyla się w płaszczyźnie n-n prostopadłej do linii śrubowej (wyznaczonej przez średnią średnicę roboczą d_s) o kąt a_Tn. Płaszczyzna n-n tworzy z płaszczyzną 0-0 przechodzącą przez oś śruby kąt y (rys. 4.4 a). Z rysunku 4.4 c można wyznaczyć związek między roboczym kątem boku gwintu a_T (w płaszczyźnie osiowej 0-0) i kątem boku gwintu a_rn w płaszczyźnie normalnej n-n. Ponieważ

GA

GF

stąd

DA    DG

Ig arn. ~Y~^tS^ar> GF = DE 1    = cosy

(4.8)

— cos;’.

^    _tg Urn

tg a_r