54551 new 40

84 4. Rozkład sił na gwincie

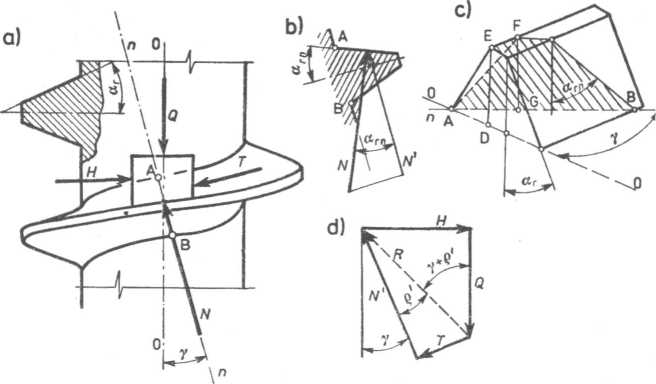
Rys. 4.4. Rozkład sił w złączu z gwintem o dowolnym zarysie przy podnoszeniu ciężaru: a) schemat złącza, b) rozkład sił w płaszczyźnie n—n, c) związek między kątem boku zarysu w płaszczyźnie osiowej a_r i kątem boku zarysu w płaszczyźnie normalnej a_rn, d) zamknięty wielobok sił

Dla samohamownych śrub złącznych kąt wzniosu gwintu y jest bardzo mały (cosy « 1), można zatem z dostateczną w praktycznych obliczeniach dokładnością 'przyjmować a_rn=a_r. Jednakże przy obliczaniu śrub o dużym kącie y, takie uproszczenie jest niedopuszczalne.

N'    1

Siła tarcia T = uN = u-= u'N' jest    raza większa od siły

COS arn    COS a_rn

określonej równaniem (4.2). Dla uproszczenia zapisu wprowadza się umowne pojęcie pozornego współczynnika tarcia

f

n

cos a_rn

= tge

(4.9)

i pozornego kąta tarcia j/=arctg p.

Przy podnoszeniu ciężaru Q na śrubie siła oddziaływania nakrętki #=    N²+T² =N' \f l+p'², tworzy z siłą Q kąt y+Q (rys. 4.4d). Stąd

siła obwodowa H wynosi

H=Q tg(y+_e').    (⁴¹°)

Podobnie przy opuszczaniu ciężaru Q (4.11)

Moment obrotowy, jaki trzeba przyłożyć, aby pokonać opory na gwincie zgodnie ze wzorami (4.4) i (4.6) wyrazić można ogólną zależnością gdzie znak „+” dotyczy podnoszenia ciężaru na śrubie lub dokręcania śruby złącznej, a znak ” — opuszczania ciężaru lub odkręcania śruby złącznej.

Moment przy dokręcaniu śruby lub nakrętki w połączeniu złącznym jest powiększony o dodatkowe opory tarcia, jakie występują na powierzchni styku łba śruby (nakrętki) z elementem łączonym. Pierścieniowa powierzchnia oporowa (rys. 4.5) jest ograniczona wewnętrznie średnicą

S ___

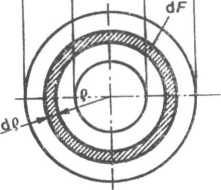
Ryp. 4.5. Schemat wyznaczenia średniego promienia tarcia

otworu przejściowego d₀ (patrz tablica 3.1) i zewnętrznie średnicą równą w przybliżeniu rozmiarowi „pod klucz” — S. Przy założeniu równomiernego rozkładu nacisków na powierzchni oporowej

p=

Q

~(s²-dl)

na elementarnym wycinku powierzchni dF = 2ngdg działa moment tarcia

d S

dM_t=Qpii dF. Stąd przyjmując granice zmienności promienia Q od "do—

Z z

dM_t = ppp dF. otrzymujemy

M_t =

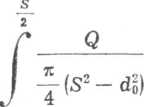
2np£² dQ=Qp-

2

S³ -dg 3(S² - d«)

(4.13)

lub oznaczając średni promień tarcia

S^:! - do S² + Sd„ + dl ^r‘ 3(S² — do)    3 (S + d„)

moment tarcia wyrazi się wzorem

M_t=Q/<r_t. (4.14)