116402

3. Siatka Karnaugha

Aby jak najbardziej zminimalizować funkcję należało zastosować siatkę Karnaugha, która wyglądała następująco:

* <d	00	01	11	10
00	1	1	0	1
01	0	0	1	1
11	0	0	1	1
10	1	1	0	0

W rezultacie otrzymaliśmy następującą funkcję:

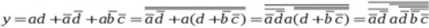
4. Schemat

Po zakończeniu przekształcania funkcji do postaci iloczynowej mogliśmy przystąpić do sporządzania schematu z użyciem wyłącznie bramek NAND oraz NOT. W efekcie pracy otrzymaliśmy następujący schemat:

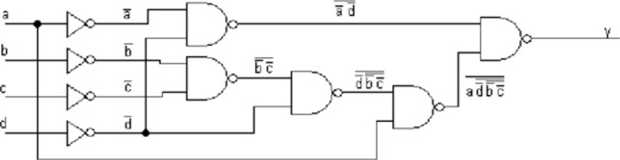
Układ ten został połączony i zweryfikowany. Zaraz po podłączeniu okazało się, że znaleźliśmy błąd, który wynikał z błędnego podłączenia jednego przewodu. Po usunięciu problemu układ działał poprawnie.

1.    Opis problemu

Naszym kolejnym zadaniem było przerobienie powyższego równani i układu tak, aby można było go zrealizować na bramkach NOR i NOT.

2.    Tabelka prawdy

Taka sama jak w punkcie 1.2.

3.    Siatka Karnaugha

Taka sama jak w punkcie I. 3.

Otrzymaną tam funkcję przekształcamy w inny sposób. y = ad +3d +aE? = 5d + a(d +E?) = a+b + S + (d+b + c)

4.    Schemat

Ilustracja graficzna powyższej funkcji wygląda następująco:

2