120767

Wobec 1) i 2) e^A jest równe sumie swego rozwinięcia

V*"

xa9*

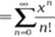
DEFINICJA 19.2 (EKSPONENTA)

Niech zeC

e' = exp z-.= t^z—

TS n!

UWAGA:

Jeśli z jest rzeczywiste eksponenta jest identyczna z e*. Można więc traktować powyższą definicję jako rozszerzenie funkcji e* na ciało liczb zespolonych. Powyższa uwaga dotyczy wszystkich zdefiniowanych dalej funkcji.

PRZYKŁAD 19.2

Niech f(x) =sinx,

Analogicznie jak w przykładzie 19.1

sinx = £(-l)‘

Ł-0

(2k + l)!

⁺ ^2n*l(U. x);

(2n+2)i

Ponieważ f^l2"*^2l(St)jest ograniczone więc

I*-'⁰'**- (Zn+lj! -Rozumując podobnie jak w przykładzie 19.1 stwierdzamy, że:

>o dla xe 95.

V*lnx=B—1 >*-£

(2n +1)!

DEFINICJA 19.3 (FUNKCJA SINUS)

Niech zeC

sin zy^(—U"

z²"*¹

(2n+l)ł

PRZYKŁAD 19.3

Niech f(x)=cosx.

Analogicznie jak w przykładzie 19.1