49665

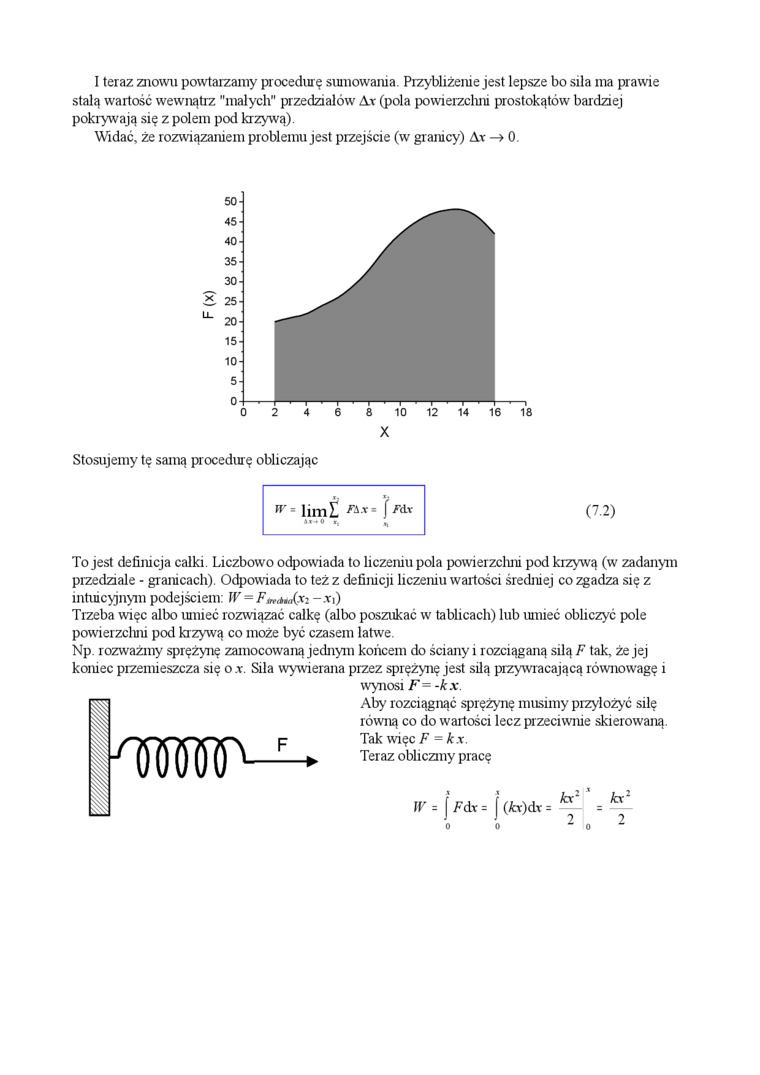
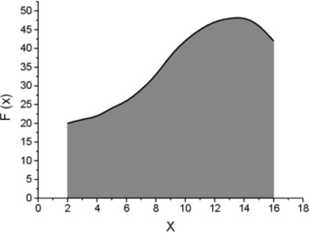
I teraz znowu powtarzamy procedurę sumowania. Przybliżenie jest lepsze bo silą ma prawie stalą wartość wewnątrz "małych" przedziałów Ar (pola powierzclini prostokątów bardziej pokrywają się z polem pod krzywa)

Widać, że rozwiązaniem problemu jest przejście (w granicy) Ar -» 0.

Stosujemy tę samą procedurę obliczając

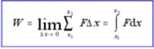
(7.2)

To jest definicja całki. Liczbowo odpowiada to Uczeniu pola powierzchni pod krzywą (w zadartym przedziale - granicach). Odpowiada to też z definicji liczeniu wartości średniej co zgadza się z intuicyjnym podejściem: W =    -xi)

Trzeba więc albo umieć rozwiązać całkę (albo poszukać w tablicach) lub umieć obliczyć pole powierzchni pod krzywą co może być czasem łatwe

Np. rozważmy sprężynę zamocowaną jednym końcem do ściany i rozciąganą silą F tak, że jej koniec przemieszcza się o ,r. Siła wywierana przez sprężynę jest silą przywracającą równowagę i

wynosi F=-k x.

Aby rozciągnąć sprężynę musimy przyłożyć silę równą co do wartości lecz przeciwnie skierowaną Tak więc F = k.x.

Teraz obliczmy pracę

kx² '    b:²