Ogólny schemat budowy modelu ekonometrycznego
Krok I
Określenie celu badań modelowych
Krok II
Specyfikacja elementów systemu i jego otoczenia
Krok III
Specyfikacja zmiennych wraz z gromadzeniem danych
Krok IV
Wybór klasy modelu
Krok V
Estymacja parametrów strukturalnych
Krok VI
Weryfikacja modelu
Krok VII
Wnioskowanie na podstawie modelu
Schemat procedury weryfikacji modelu ekonometrycznego otrzymanego metodą najmniejszych kwadratów (ciągle wersja wstępna)
y = f (x1,x2,...,xk, ε) = ao + a1 x1 +...+ ak xk+εi
gdzie:
y - zmienna objaśniana,
xi - zmienna objaśniająca,
ε - składnik losowy,
Etap I
Badanie dopuszczalności modelu ze względu na wartości współczynników zmienności (V) oraz zbieżności (![]()
):
![]()
,
gdzie: ![]()
- błąd standardowy reszt, ![]()
- wartość średnia zmiennej Y.
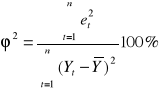
,
gdzie: ![]()
- kwadrat reszt (![]()
, ![]()
- obserwacje zmiennej objaśnianej, ![]()
- wartości zmiennej objaśnianej z modelu). Możliwe jest przedstawienie alternatywne za pomocą współczynnika determinacji: ![]()
.
W sposób arbitralny ustala się wartość graniczną ![]()
(jest to zazwyczaj wielkość około 10%), oraz około 60% dla R2.
Badanie koincydencji
Etap II
Badanie istotności układu współczynników (w oparciu o statystykę F-Snedecora)
Istotność układu współczynników regresji.
Stawiamy hipotezę:
![]()
przeciwko hipotezie alternatywnej
![]()
.
Hipotezę tę weryfikujemy w oparciu o statystykę
![]()
Statystyka F, przy prawdziwości hipotezy zerowej ma rozkład F-Snedecora o (k) stopniach. licznika i (n-k-1) stopniach mianownika.
Etap III
Dla każdego parametru równania regresji (j=0,1,...,k) stawiana jest hipoteza ![]()
przeciwko hipotezie alternatywnej ![]()
.
Hipotezę weryfikujemy w oparciu o statystykę
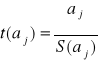
,
Statystyka ta przy prawdziwości hipotezy zerowej ma rozkład t-Studenta o (n-k-1) stopniach swobody.
Jeżeli dla jakiejś zmiennej objaśniającej j przyjmowana jest hipoteza zerowa, to daną zmienną objaśniającą usuwamy z modelu.
Wyeliminowanie jakiejkolwiek zmiennej objaśniającej wymaga powtórnego formułowania modelu i powtórzenia etapu I.
Brak eliminacji jakiejkolwiek zmiennej objaśniającej pozwala na przejście do etapu II.
Etap IV Badanie normalności reszt
Zweryfikuj hipotezę, że reszty mają rozkład normalny o wartości oczekiwanej równej 0. Wybór testu zależy od wielkości próby (ilości obserwacji)
Etap V
Badanie autokorelacji składnika losowego.
Stawiana jest hipoteza zerowa ![]()
wobec hipotezy alternatywnej ![]()
, gdzie ![]()
jest współczynnikiem autokorelacji (współzależnością korelacyjną składników losowych ![]()
oraz ![]()
, ![]()
, najczęściej stosowana jest wartość ![]()
):
![]()
Ponieważ wartości składników losowych nie są bezpośrednio obserwowalne to zamiast nich stosuje się obserwacje reszt ![]()
i oblicza wartość statystyki Durbina-Watsona:

Tablice testu Durbina-Watsona (patrz np. Cz. Domański Testy statystyczne, PWE 1990) podają wartości krytyczne ![]()
oraz ![]()
dla wybranych wartości liczby obserwacji n oraz liczby szacowanych parametrów k.
Hipotezę H0 odrzucamy jeżeli zachodzi nierówność ![]()
, co oznacza istnienie istotnej dodatniej autokorelacji. Zachodzenie nierówności ![]()
nie daje podstaw do odrzucenia hipotezy zerowej (zachodzenie nierówności ![]()
nie pozwala na rozstrzygnięcie tej kwestii).
Jeżeli występuje korelacja ujemna (![]()
) to w miejsce statystyki d stosujemy statystykę ![]()
i postępujemy dalej jak ze statystyką d.
Jeżeli stwierdzono autokorelację składnika losowego to można:
wprowadzić do modelu nowe zmienne objaśniające lub zmienić jego postać, albo
próbować wyeliminować autokorelację poprzez tzw. przekształcenie Cochrana-Orcutta.
Przekształcenie Cochrana-Orcutta polega na przejściu od modelu ![]()
, ![]()
, do modelu ![]()
, ![]()
, przy czym:
![]()
, dla ![]()
,
![]()
dla ![]()
,
gdzie ![]()
oznacza wartość współczynnika korelacji pomiędzy resztami modelu dla ![]()
.
Jeżeli nie nastąpiło odrzucenie hipotezy zerowej o braku autokorelacji składnika losowego to przechodzimy do następnego etapu.
Etap VI
Badanie symetrii składnika losowego.
Niech m oznacza liczbę odchyleń in plus (lub zamiennie in minus) pomiędzy wartościami obserwowanymi Y a wyliczonymi w modelu (teoretycznymi) ![]()
. Hipoteza dotycząca symetrii składnika losowego przedstawia się następująco:
H0: (frakcja reszt dodatnich = ½), przeciwko hipotezie alternatywnej: H1: (frakcja reszt dodatnich <> ½),
Weryfikujemy ją testem istotności:
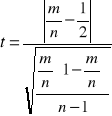
,
który dla ![]()
ma rozkład studenta o n-1 stopniach swobody, natomiast dla n > 30 ma rozkład normalny.
Jeżeli hipoteza zerowa jest odrzucana to należy zmodyfikować model (np. nowa postać analityczna).
Jeżeli hipoteza zerowa nie jest odrzucana to przechodzimy do następnego etapu.
Etap VII
Badanie losowości reszt modelu.
O losowości składnika losowego ![]()
sądzimy na podstawie reszt ei , stawiając hipotezę zerową ![]()
jest czysto losowy, wobec hipotezy alternatywnej ![]()
nie jest czysto losowy.
Weryfikujemy tę hipotezę np. testem serii zliczając ilość serii K tych samych znaków reszt w modelu. Wartość K konfrontujemy z wartością krytyczną ![]()
z tablic testu serii:
![]()
lub ![]()
.
Jeżeli ![]()
to hipotezę o losowości składnika losowego odrzucamy i musimy model zmodyfikować.
Jeśli hipoteza o losowości składnika losowego jest prawdziwa to przechodzimy do następnego etapu.
Etap VIII
Badanie stacjonarności składnika losowego.
O stacjonarności składnika losowego ![]()
sądzimy na podstawie reszt ei , stawiając hipotezę zerową ![]()
jest stacjonarny, wobec hipotezy alternatywnej ![]()
nie jest stacjonarny.
Zatem, szacujemy wartość zależności stochastycznej między ![]()
a t (![]()
) poprzez współczynnik korelacji r między t a et:
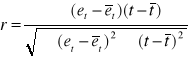
Hipotezę zerowa weryfikujemy testem t-Studenta o n-2 stopniach swobody:
![]()
.
Odrzucenie hipotezy zerowej wymaga zmodyfikowania modelu.
Etap IX
Badanie homoscedastyczności.
Równość wariancji w podpróbach homogenicznych ze względu na wariancję składnika losowego można przeprowadzić w oparciu o test Goldfelda-Quandta:
Dla podprób o najmniejszej i największej wariancji (o liczebnościach odpowiednio ![]()
,![]()
) budujemy równania regresji,a następnie stawiamy hipotezę zerową:
![]()
przy kontrhipotezie: ![]()
Hipotezę weryfikujemy w oparciu o statystykę:
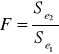
gdzie:
![]()
-wariancja reszt modelu regresji dla podpróby o najmniejszej wariancji,
![]()
-wariancja reszt modelu regresji dla podpróby o największej wariancji.
Przy prawdziwości hipotezy zerowej statystyka F ma rozkład F-Snedecora o (![]()
) stopniach swobody licznika i o (![]()
) stopniach swobody mianownika.
Etap X
Analiza wpływów
Etap XI
Prognoza i jej ocena.
Wyszukiwarka
Podobne podstrony:
ogolny schemat budowy modelu ekonometrycznego
Schemat budowy modelu ekonometrycznego KYBRZMJFNH4WDSL6VDZLDWXN5SPAVPIB5YJ7BWA
etapy budowy modelu ekonometrycznego VGPJGEDNN54UQ3OJEEJJIDMNQSBBK7AH72X2J6I
R3-3 [Schematy budowy aktów normatywnych (PL)], Budowa aktu normatywnego
TECHNOLOGICZNE UWARUNKOWANIA BUDOWY NUMERYCZNEGO MODELU RZEŹ, TECHNOLOGICZNE UWARUNKOWANIA BUDOWY NU
Schemat budowy masztu nadawczego
notatek pl schemat budowy komor Nieznany
PROCES BUDOWY MODELU ORGANIZACJI
R2-6 [Precedens prawotwórczy], Schemat budowy precedensu prawotwórczego
Schemat budowy komputera
Schemat budowy standardu opieki piel
kubica, biologia z elementami mikrobiologii, schemat budowy bakterii
Schematy budowy reaktorów wolnej energii zostały ujawnione
więcej podobnych podstron