Politechnika Warszawska
Wydział Inżynierii Lądowej
Instytut Konstrukcji Budowlanych
Konstrukcje Betonowe Specjalne
„Zbiornik na wodę”
Prowadzący: dr inż. Krzysztof Donten
Wykonał:
Michał Ćwik
gr. KBI sem. 9
Data: 09.04.2005
dane do projektowania:
rozpiętość: L = 7.40 m
szerokość podparcia: a = 0.50 m
średni współczynnik obciążenia: γ = 1.25
obciążenie charakterystyczne (z ciężarem własnym): qk = 40 kN/m
dane materiałowe:
beton B37:
fctm = 2.9 MPa
fck = 30 MPa
fcd = 20 MPa
fctd = 1.33 MPa
Ecm = 32 MPa
stal (zbrojenie główne) A-III; 34GS
fyk = 410 MPa
fyd = 350 MPa
ftk = 550 MPa
Es = 200 GPa
ξeff,lim = 0.53
stal (strzemiona) A-0; St0S-b
fyk = 220 MPa
fyd = 190 MPa
ftk = 300 MPa
Es = 200 GPa
ξeff,lim = 0.63
rozpiętość obliczeniowa belki:
an1 = an2 = an = min(0.5⋅a; 0.5⋅h)
an1 = an2 = an = min(0.5⋅50; 0.5⋅60) = 25 cm
leff = ln + an1 + an2
leff = 7.40 + 0.25 + 0.25 = 7.90 m
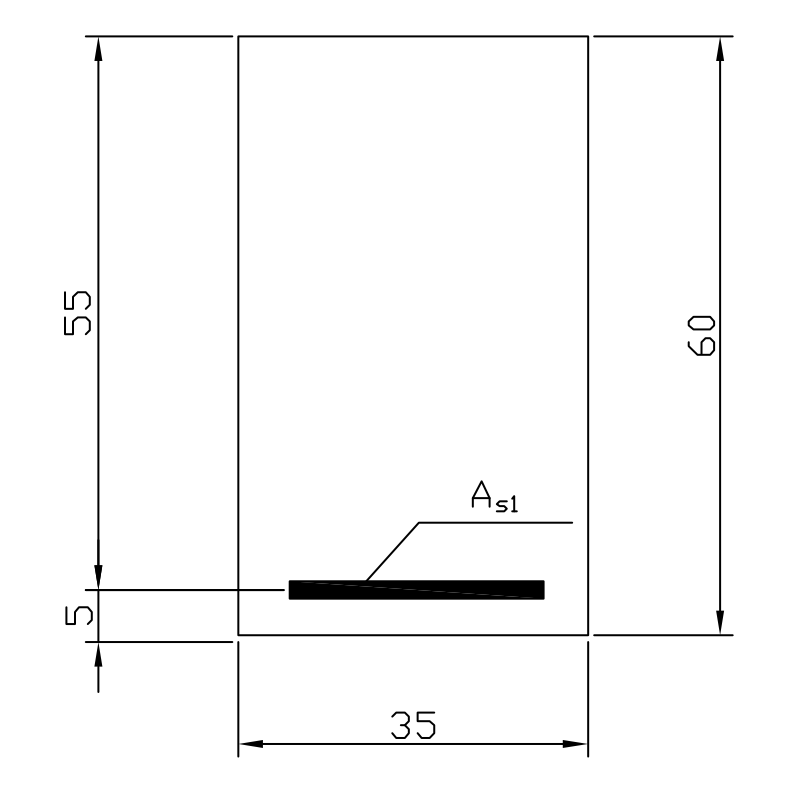
przekrój belki:
h = 60 cm
b = 35 cm
d = 55 cm
a1 = 5 cm
![]()
= 0.1 ÷ 0.067 ![]()
![]()
= 0.076 ![]()
= 1.71
obciążenie działające na belkę:
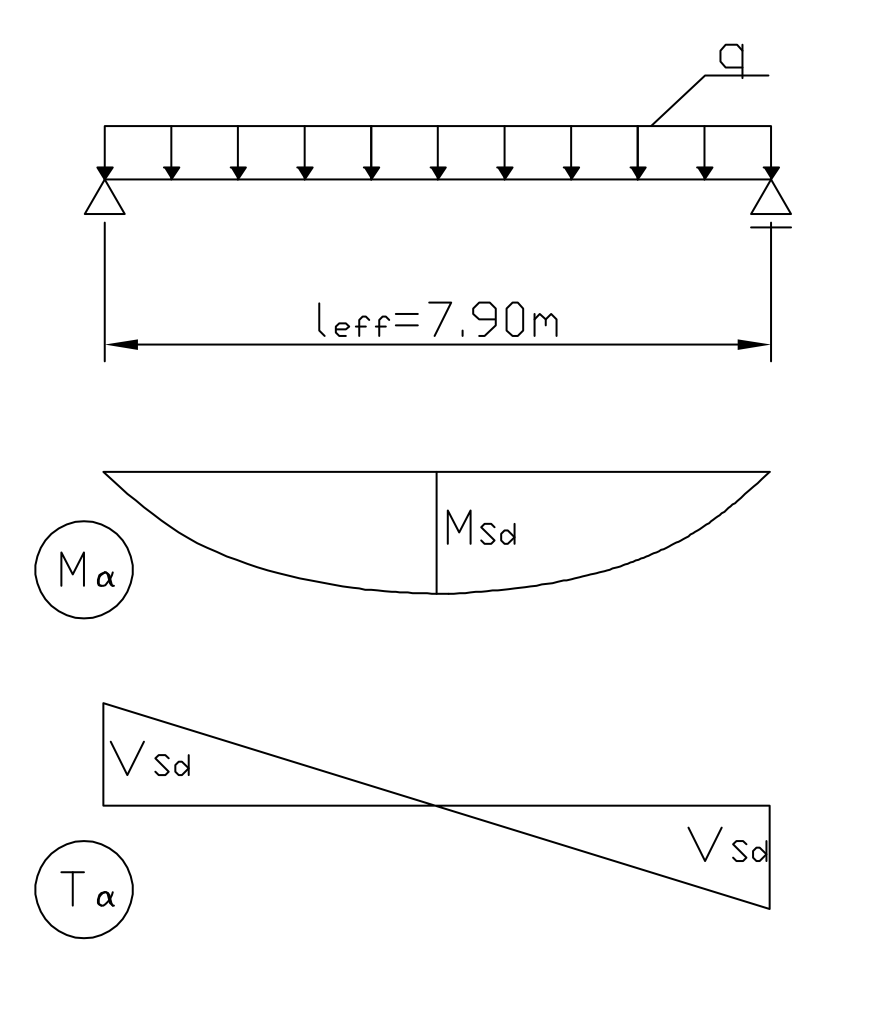
q = qk ⋅ γ
q = 40 ⋅ 1.25 = 50 kN/m
Msd = Msd = ![]()
Msd = ![]()
= 390.06 kNm
Vsd = ![]()
Vsd = ![]()
= 197.50 kN
pole powierzchni zbrojenia głównego:
As1,min = 0.0013 ⋅ b ⋅ d
As1,min = 0.0013 ⋅ 35 ⋅ 55 = 2.5 cm2
As1,min = 0.26 ⋅![]()
⋅b ⋅ d
As1,min = 0.26 ⋅![]()
⋅35 ⋅ 55 = 3.54 cm2
As, min = kc ⋅ k ⋅ fct,eff ⋅![]()
kc = 0.4
k = 1
Act = 0.5⋅b⋅h = 1050 cm2
fct,eff = fctm = 2.9 MPa
σs,lim = 200 MPa
As, min = 0.4 ⋅ 1 ⋅ 2.9 ⋅![]()
= 6.09 cm2
xeff,lim = ξeff,lim ⋅ d
xeff,lim = 0.53 ⋅ 55 = 29.2 cm
As1,max = 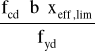
As1,max = ![]()
= 58.4
maksymalny stopień zbrojenia:
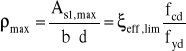
![]()
= 0.03 = 3%
obliczenie potrzebnego zbrojenia:
μsc = ![]()
μsc = ![]()
= 0.184
dla μsc = 0.184 odczytana z tablicy wartość ζ = 0.898
As1 = 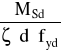
As1 = ![]()
= 22.56 cm2
przyjęto: zbrojenie główne 6φ22 ⇒ As1 = 22.80 cm2
strzemiona φ8
minimalna odległość między prętami:
s1 ≥ φ
s1 ≥ 22 mm
s1 ≥ dg + 5
s1 ≥ 16 + 5 = 21 mm
otulina:
cnom = cmin + Δc cmin ≥ φ; Δc =5
cnom = 22 + 5 = 27 mm
a1 = 0.5 ⋅ φ + φw1 + cnom = 0.5 ⋅ 22 + 8 + 27 = 46 mm
przyjeto a1 = 50 mm
stopień zbrojenia:
![]()
![]()
= 0.012 = 1.2%
nośność na ścinanie odcinków I rodzaju:
VRd1 = [0.35 ⋅ k ⋅ fctd ⋅ (1.2 + 40 ⋅ ρL) + 0.15 ⋅ σcp]⋅bw ⋅ d
k = 1.6 - d = 1.6 - 0.55 = 1.05
ρL = ρ = 0.01
σcp = 0
VRd1 = [0.35 ⋅ 1.05 ⋅ 0.133 ⋅ (1.2 + 40 ⋅ 0.01) + 0]⋅35 ⋅ 55 = 150.54 kN
c0 = ![]()
c0 = ![]()
= 0.94 m = 94 cm
z = 0.9 ⋅ d
z = 0.9 ⋅ 55 = 49.5 cm
c0 ≥ z ⋅ ctgθ; przyjęto ctgθ = 1.75
c0 ≥ 49.5 ⋅ 1.75 = 87 cm
ν = 0.6 ⋅ (![]()
)
ν = 0.6 ⋅ (![]()
) = 0.53
VRd2 = 0.5 ⋅ ν ⋅ fcd ⋅ bw ⋅ z
VRd2 = 0.5 ⋅ 0.53 ⋅ 2 ⋅ 35 ⋅ 49.5 = 918.23 kN
nośność na ścinanie odcinków II rodzaju:
VRd2 = ν ⋅ fcd ⋅ bw ⋅ z ⋅ ![]()
VRd2 = 0.53 ⋅ 2 ⋅ 35 ⋅ 49.5 ⋅ ![]()
= 1168.65 kN
dla pojedynczych strzemion φ8 ⇒ Asw1 = 2 ⋅ 0.42 ⋅ π = 1.01 cm2
VRd3 = 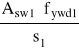
⋅ z ⋅ ctgθ
VSd ≤ VRd3
s1 = 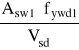
⋅ z ⋅ ctgθ
s1 = ![]()
⋅ 49.5 ⋅ 1.75 = 8.42 cm
s1 ≤ smax = 40 cm
przyjęto s1 = 80 mm
stopień zbrojenia strzemionami:
ρw1,min = 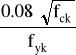
ρw1,min = ![]()
= 0.0013 = 0.13%
ρw1 = ![]()
ρw1 = ![]()
0.0036 = 0.36%
szerokość rys prostopadłych do osi elementu wg załącznika D:
![]()
dla ρ > 1% ⇒ ζ = 0.8; MSd = 312.05 MPa - moment dla γ = 1
![]()
= 31.436 kN/cm2 = 314.36 MPa
ponieważ średnica prętów zbrojenia (φ = 22 mm) jest mniejsza od maksymalnej (φ = 24 mm), szerokość rys prostopadłych uznaje się za ograniczoną do wlim = 0.3 mm
szerokość rys ukośnych:
ponieważ strzemiona prostopadłe do osi elementu są wykonane ze stali A-0 o średnicy
φ = 8 mm i zapewniają przy ctgθ = 1.75 wystarczającą nośność na ścinanie sprawdzanie szerokości rys ukośnych nie jest wymagane
podstawowa długość zakotwienia zbrojenia:
lb = ![]()
; dla betonu klasy B37 przyjęto fbd = 3.0
lb = ![]()
= 64.2 cm
obliczeniowa długość zakotwienia zbrojenia:
lb,min = 0.3 ⋅ lb > 10 ⋅ φ lub 100 mm
lb,min = 0.3 ⋅ 64.2 = 19.3 cm > 10 cm
As,req = 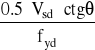
As,req = ![]()
= 4.94 cm2
lbd = αa ⋅ lb ⋅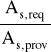
≥ lb,min; αa = 1 - dla prętów prostych
lbd = 1 ⋅ 64.2 ⋅![]()
= 13.9
przyjęto długość zakotwienia lbd = 20 cm
ugięcia elementu:
obliczenie naprężeń w zbrojeniu rozciąganym metodą naprężeń liniowych:
![]()
![]()
x = 18.2 cm
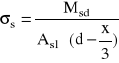

= 313.30 MPa
sprawdzenie konieczności obliczania ugięć:
wartość z tablicy nr 13 należy pomnożyć przez współczynnik a (obliczenia przy założeniu, że belka pracuje w przekryciu dachowym):
a = ![]()
dla 6 m < leff < 10m ⇒ alim = 40 mm
a = ![]()
= 0.61
z tablicy 13 dla ρ = 1.2% maksymalna wartość ![]()
dla której nie trzeba obliczać ugięć, dla powyższych założeń wynosi:
a ⋅ 24.2 = 14.66
obliczeniowa wartość ![]()
=![]()
=14.36 czyli sprawdzenie ugięć nie jest konieczne
NIEZAWODNOŚĆ KONSTRUKCJI
DANE
b = 35 cm
d = 55 cm
As = 22.80 cm2
fck = 30 MPa
fyk = 220 MPa
obciążenie zmienne charakterystyczne gk = 20 kN/m
obciążenie stałe charakterystyczne qk = 20 kN/m
Strona - 3 -
Wyszukiwarka
Podobne podstrony:
Projekt niezawodność - Ćwik, podstawowy, Praca 6 - Projekt
praca projektowa nr I
Projekt 1 21 09, Praca projektowa nr 1 úukasz Pluta, Praca projektowa nr 1
Praca projektowa Słup stalowy osiowo ściskany, szkola, szkola, sem 5, konstrukcje metalowe
Praca projektowa
Projekt 1 niezawodność
Praca projektowa z informatyki
Niezawodność Projekt Ćwik
1 2 Dystrybuanta, Niezawodność konstr, niezawodność, 1 projekt
karta inf praca przejściowa projekt
Biznes plan - praca zaliczeniowa, Studia - materiały, semestr 7, Zarządzanie, Marketing, Ekonomia, F
Zadanie 01 statystyka, Niezawodność konstr, niezawodność, 1 projekt
Praca Przejściowa-1, Pomoce Naukowe 2, SEMESTR 6, technologia referat, technologia -projekt
Projekt i załoŻenia techniczne budowy małej stacji paliw płynnych praca inzynierska budownictwox
Grzybice skory, dermatologia, Praca do projektu
więcej podobnych podstron