II Inf.	METODY OPISU WŁAŚCIWOŚCI DYNAMICZNYCH ELEMENTÓW AUTOMATYKI. OPIS PRZESTRZENI STANÓW	27.04.98
	Jasiński Jarosław Głąb Andrzej

Coraz częściej stosuje się opis właściwości układu z użyciem współrzędnych stanu. Opis ten można w wielu przypadkach uważać za równoważny transmitancji operatorowej dla układów jednowymiarowych i macierzy transmitancji dla układów wielowymiarowych. Jednak równania stanu, chociaż trudniejsze niż transmitancje do interpretacji fizycznej i niemożliwe do bezpośredniego określenia w drodze pomiarowej, są wygodniejsze do celów modelowania analogowego i cyfrowego oraz do projektowania układów wielowymiarowych.

Wielkości charakteryzujące zachowanie się układu nazywamy współrzędnymi, a najmniejszy liczebnie zespół współrzędnych, wystarczający łącznie za znajomością wielkości wejściowych do określenia zachowania się układu w przyszłości, nazywamy wektorem stanu układu.

Rozważając np. poruszający się element o masie m i współczynniku tarcia k_p, opisany liniowym równaniem różniczkowym drugiego rzędu. Wyznaczenie przebiegu położenia y(t) elementu dla czasów t>t₀ wymaga znajomości położenia y(t₀) i prędkości y'(t₀) (współrzędne te określają stan układu i można je rozumieć jako podsumowanie zachowania układu w czasie t<t₀) oraz znajomości przebiegu wielkości wejściowych (np. sił) dla t>t₀.

W ogólnym opisie układów wielowymiarowych poszczególne wielkości określone są w postaci wektorów i oznaczają

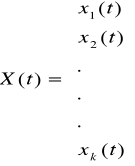
- wektor wejść, którego składowymi są poszczególne wielkości wejściowe x₁(t),...,x_k(t),

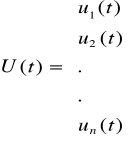
- wektor stanu, którego składowymi są współrzędne stanu u₁(t),...,u_n(t) - liczba współrzędnych jest zawsze równa rzędowi układu.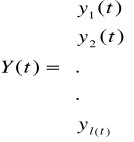
- wektor wyjść, którego składowymi są poszczególne wielkości wyjściowe y₁(t),...,y_l(t).

W przypadku szczególnym wielkości te mogą się pokrywać, np. w omawianym przykładzie położenie y(t), ale często są to odmienne wielkości.

Nie należy utożsamiać liczby współrzędnych stanu z liczbą wielkości wyjściowych. Układ może mieć tylko jedną wielkość wyjściową, a być opisywany np. równaniem czwartego rzędu i wówczas wektor stanu, określający jednoznacznie stan układu w chwili t₀, zawierać będzie cztery współrzędne stanu.

Zbiór wszystkich możliwych wartości wektora stanu U(t) w chwilach t tworzy przestrzeń stanów układu (przestrzeń fazową). Zbiór wartości wektora stanu układu w kolejnych chwilach czasu tworzy w tej przestrzeni krzywą, zwaną trajektorią stanu układu (trajektorią fazową).

Równanie stanu układu zapisuje się zwykle w postaci

U '(t)=F[U(t),X(t)]

z n warunkami początkowymi

U(t₀)=U₀,

przy czym U '(t)=dU(t)/dt.

Równanie stanu układu jest zawsze równaniem różniczkowym pierwszego rzędu, w ogólnym przypadku nieliniowym i zależnym jawnie od czasu, a F jest n- elementową funkcją wektorową.

Równanie wyjścia układu ma postać

Y(t)=G[U(t),X(t)],

przy czym G jest l- elementową funkcją wektorową. Nie jest to równanie różniczkowe, gdyż cała dynamika układu opisana jest równaniem stanu, jest natomiast zależne od czasu.

Równania stanu zapisuje się zwykle skrótowo w postaci macierzowej :

U '(t) = A(t)U(t) + B(t)X(t) ,

Y(t) = C(t)U(t) + D(t)X(t) ,

przy czym

A(t) - macierz układu stopnia n *n,

B(t) - macierz wejść stopnia n *k,

C(t) - macierz wyjść stopnia l *n,

D(t) - macierz transmitancyjna układu stopnia l *k.

W przypadku szczególnym, gdy układ jest liniowy stacjonarny, pochodne cząstkowe względem zmiennych u₁,...,u_n,x₁,...,x_k nie zawierają czasu i pochodne cząstkowe względem czasu są równe zeru. Elementy macierzy są wówczas stałe i równanie stanu układu można zapisać w postaci

U '(t)=AU(t)+BX(t),

odpowiadającej liniowemu równaniu różniczkowemu o stałych współczynnikach, które w razie potrzeby można transformować przy użyciu przekształcenia Laplace'a, natomiast równanie wyjścia układu przyjmuje postać

Y(t)=CU(t)+DX(t).

Analizując :

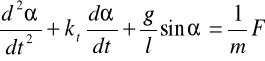
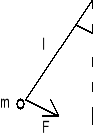
gdzie : prędkość kątowa

,

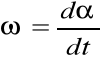
przyspieszenie kątowe

,

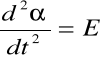
α- kąt wychylenie wahadła (dla małego kąta
) , k_t - współczynnik tarcia, g=9.81 m/s², l=1m, m=1kg.

Gdy na wahadło nie działa żadna siła zewnętrzna (wykresy I ) ,wówczas prawą stronę równania przyrównuję do zera :

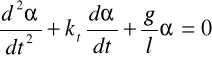
Wejściem jest siła przyłożona do wahadła, natomiast wyjście to położenie kątowe.

Jak widać na dołączonym wykresie trajektorii fazowej na płaszczyźnie fazowej punkt początkowy ma współrzędne (α ,0). Punkt końcowy (punkt równowagi) przyjmuje wartość (0,0)- jest to ognisko stabilne. Niezależnie od wartości początkowych zawsze będzie ten sam typ trajektorii fazowej.

Aby wyznaczyć transmitancję układu, gdzie siła jest wielkością wejściową, a

wyjściową jest kąt :

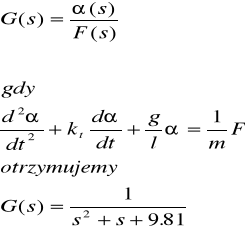
Wyznaczając równania stanu pamiętając o wspomnianej wcześniej postaci równań stanu w formie macierzowej :

x = Ax + Bu

y = Cx + Du

gdzie A,B,C,D są macierzami, x- wektor zmiennych stanu (dla wahadła dwu elementowy),

y- wektor wyjść (dwu elementowy), u to wektor wejść.

Zmiennymi stanu są : x₁- kąt wychylenia wahadła, x₂- prędkość kątowa, u= F.

+Wówczas:

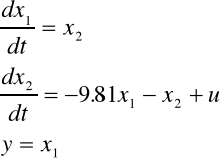
W postaci macierzowej :

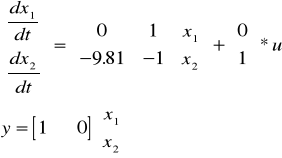
y- równanie wyjścia.

Wartości własne układu (bieguny transmitancji):

λ - pewna liczba, I- macierz jednostkowa, A- macierz.

Analizując :

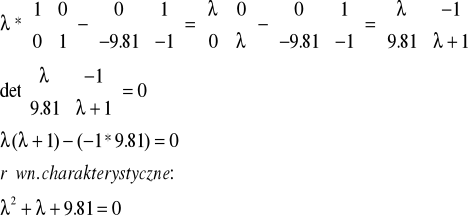
Dokonując rozwiązania naszego równania charakterystycznego zauważamy istnienie dwóch pierwiastków :

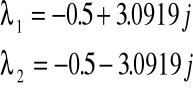
Pierwiastkami są wartości zespolone, sprzężone. Układ jest stabilny, bo część rzeczywista jest ujemna oraz oscylacyjny ze względu na istnienie członu urojonego.

Rozpatrujemy przypadek, gdy k_t=0 (wykresy II ), czyli przy założeniu, że wahadło jest idealne. Transmitancja wygląda wówczas następująco :

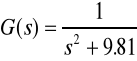
Jak widzimy wychylenia wahadła są stałe, także prędkość w danych położeniach jest niezmieniona. Analizując wykres trajektorii fazowej zauważamy, że układ jest na granicy stabilności (ponieważ nie ma części rzeczywistej w pierwiastkach równania; drgania wahadła nie ulegają zmianie w czasie) :

s1= 3.1321j

s2= -3.1321j .

Wyznaczam następnie taką wartość k_t, dla której układ będzie członem aperiodycznym:

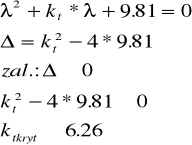
Dla wyżej obliczonej wartości k_t układ przestaje być oscylacyjnym.

Spoglądając na trajektorię fazową zauważamy, że układ jest stabilny (własności własne rzeczywiste) i bez oscylacji.

Z położenia 0.5 oraz prędkości 0 wahadło wykonuje pół pchnięcia i zatrzymuje się w punkcie równowago (0,0).

Rozpatrujemy przypadek, gdy k_t=7 (wykresy III ).

Transmitancja wygląda wówczas następująco :

Jak widzimy z wykresów wahadło nie wykonuje oscylacji ,wraca do położenia równowagi. Analizując wykres trajektorii fazowej ,oraz wykresy zer i biegunów zauważamy, że układ jest stabilny ,a odpowiedź układu jest aperiodyczna (ponieważ bieguny nie posiadają części urojonych ,a części rzeczywiste mają ujemne) :

s1= -5.06

s2= -1.94

---