METODY OPISU CIĄGŁYCH LINIOWYCH JEDNOMIAROWYCH OBIEKTÓW STEROWANIA

1. Równania różniczkowe opisujące jednowymiarowe obiekty sterowania ( w szczególności WE-WY).

2. Odpowiedź jednostkowa (skokowa).

3. Odpowiedź impulsowa.

4. Transmitacja operatorowa.

5. Transmitacja widmowa.

6. Metoda przestrzeni fazowej i płaszczyzny fazowej.

7. Metoda zmiennych stanu.

8. Charakterystyki częstotliwościowe.

2.Przedstawia jak zachowuje się obiekt kiedy na WE pojawia się sygnał skoku (wymuszenie).

3.Odpowiedź obiektu na krótkotrwały impuls(np. doprowadzam auto do jakiejś prędkości, przychodzi podmuch wiatru i wytrąca, muszę ulepszyć, zaplanować sterowanie.

4.Transformata Laplace'a.

5-6-7-8.Bardzo złożone.

Dlatego tak dużo opisów, bo różnie są wygodne w różnych analizach.

Matematyczna zmiana stanu - wiemy nie tylko co dzieje się na zewnątrz, ale także wewnątrz.

Charakterystyką(Odpowiedzią) skokową:

H(t) jednowymiarowego układu (obiektu) liniowego stacjonarnego, nazywać będziemy odpowiedź tego układu na wymuszenie w postaci jednostkowej funkcji skokowej 1(t), przy zerowych warunkach początkowych.

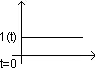
←impuls

Charakterystyką( Odpowiedzią) Impulsową

G(t)liniowym układu( Obiektu) liniowego, stacjonarnego nazywać będziemy odpowiedź tego układu na wymuszenie w postaci funkcji Diraca (t), przy zerowych warunkach początkowych.

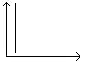
δ(t) ←impuls o nieskończonej amplitudzie, duży impuls,

o dużym czasie trwania.

Transmisją operatorową:

G(s) liniowym układu (Obiektu) liniowego stacjonarnego nazywać będziemy wartość określoną jako stosunek transformaty wymuszenia U(s) tego układu przy zerowych warunkach początkowych. G(s) =Y(s) / U(s)

TYPOWE CZŁONY LINIOWE

- Człon proporcjonalny

- Człon inercyjny I rzędu

- Człon całkujący idealny( na WY jest całka)

- Człon całkujący z inercją( to samo, tylko zaburzone)

- Człon różniczkujący( na WY pochodna sygnału WE)

- Człon różniczkujący z inercją( to samo ale zaburzony)

- Człon oscylacyjny( złożenie członów inercyjnych inercyjnych rzędu)

- Człon oscylacyjny II rzędu

- Człon opóźniający( to co na WE opóźnione na WY)

CZŁON BEZINERCYJNY

( proporcjonalny wzmacniający)

Równanie różniczkowe WE/WY: y= ku

k - współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia w stanie ustalonym.

T - stała czasowa = 0

Charakterystyka skokowa: g(t) t

h(t) = k1(t)

Charakterystyka impulsowa: h(t)

h(t) = k δ(t) t

Transmitacja:

Gi(s) = k

Kierunek przepływu prądu

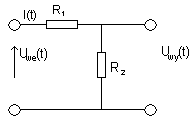
**Przykład 1: Wybieram wielkości WE i WY CZWÓRNIK czwórnika, zakładam jeszcze, że (Dzielnik jest nieobciążony.

Napięcia)

I(t) - prąd płynie, wiedzieć to musze, aby znać zależności między U_we(t) i U_wy(t).

U_we(t) = I(t) * (R₁ + R₂)

U_wy(t) = I(t) * R₂ => I(t) = ....... wyliczam I(t) i podstawiam

R₁ + R₂

U_we(t) = U_wy(t) Schemat postępowania: Wypisywanie równań opisuje

R₂ opisuje zachowanie się układu.

R₂

U_wy(t) = U_we(t)

R₁ + R₂

**Przykład 2:

PRĄDNICA TACHOMETRYCZNA PRĄDU STAŁEGO

(Jazda autem prędkościomierz przekłada prędkość obrotu kół na napiecie i pokazuje na prędkościomierzu).

Tu przychodzi strumień

Wzbudzenia(prądnica)

Nieobciążona, poruszam się w liniowym zakresie magnesowania

E(t) = U(t)

E(t) = C_E Ø Ω(t)

U(t) = C_E Ø Ω(t)

y(t) = k * U(t)

Najprostrzy człon proporcjonalny, bezinercyjny

CZŁON INERCYJNY:

(piec)

(Jak funkcja określona w czasie

I - pochodna mówi o prędkości zmian

II - pochodna o przyspieszeniu)

.

Równanie różniczkowe WE/WY: Ty + y = ku

k - współczynnik wzmocnienia określany jako stosunek odpowiedzi y do wymuszenia u w stanie ustalonym.

T - stała czasowa.

Charakterystyka skokowa:

h(t) = k( 1 - ex [(-1)/T]) 1(t)

Odpowiedź impulsowa:

g(t) = K/T ex [(-1)/T] 1(t)

Transmitacja:

k

G_s =

1 + sT

kierunek przepływu prądu

**Przykład 1:

CZWÓRNIK RC

Nieobciążony.

U_we(t) = RI(t) + 1/C ∫ I(t) dt

U_we(t) = RI(t) + U_wy(t)

U_wy(t) = 1/C ∫ I(t) dt

d U_wy(t) 1

= * I(t) tj. funkcja czasu

dt C

RC d U_wy

U_we(t) = . * + U_wy

T y + y dt

Oznacza to, że jak włącze napięcie na WY nie pojawi się niezwłocznie, tylko będzie narastać.

Im stała czasowa mniejsza, tym szybciej zostanie osiągnięty stan przez WY.

**Przykład 2:

ELEMENT GRZEWCZY:

P - moc jest funkcją czasu P(t); energia dostarczana do grzejnika

dt - mały czas (delta t) energia ta rozkłada się na ciepło

dodawane i wydalane

P(t)dt = c*m *d Θ(t) + α
S Θ dt α - stała

S - powierzchnia grzejnika

Θ - ilość ciepła proporcjonalna do

To co się kumuluje to co się rozprasza temp, zmienia się w czasie

w grzejniku

Mamy bilans cieplny:

P(t)dt = c*m*d Θ(t) + αS*Θ(t) dt

1 c*m d*Θ(t) .

* P(t) = * + Θ(t) k*u(t) = T * y + y

α*S α * S dt

**Przykład 3:

GENERATOR

PRĄDU STAŁEGO

Nieobciążony

I_u(t) - prąd wzbudzenia

d*I*w(t)

L + R*I*w(t) = Uw(t)

dt

d*E(t) d*I(t)

= K

dt dt

L d*e(t) R

* + E(t) = Uw(t)

K dt K

Podsumowanie:

Co uzyskujemy?

Układy o różnych naturach podlegają pod te same równania jak odrzuce skale i jednostkę MATEMATYKA jest wszędzie.

---