1. Modelowanie  -  cele, etapy, zasady.

SFORMUŁOWANIE CELÓW

Pytanie po co to robię? Co chce zbadać, wykryć? Do czego będzie mi to służyć?

1.Opis i wyjaśnienie działania mechanizmu systemu - model FENOMELOGICZNY

2.Przewidywanie zachowania systemu w przyszłości i przy różnych warunkach, oddziaływanie na system - model PROGNOSTYCZNY.

3.Wybór właściwych oddziaływań WE spełniających określone warunki - model DECYZYJNY.

4.Wybór struktur, lub parametrów spełniającego określone zadania - model NORMATYWNY.

Ad1. Tworzenie Modeli i modelowanie.

Badamy system po to, żeby na niego oddziaływać. Musimy stworzyć opis/model takiego urządzenia, aby z niego korzystać.

Modelowanie: Przebadać model empirycznie, jak coś nie gra zmienić program, uprościć, skomplikować model. Im więcej powiązań z otoczeniem, z jakim dany obiekt funkcjonuje, tym bardziej skomplikowany (skomplikowane algorytmy itp.).

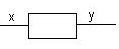
Tworzenie modeli:

I Przykład(hipotetyczny.)

x- ilość produkcji y- koszt

y = F(x) - model tego systemu (ekonomicznego)

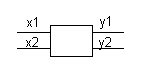
II Przykład: y1 = F(x1,x2)

2 wierze destylacyjne, y2 = F(x1,x2)

które mogą robić Podanie takiej

to samo zależności WE/WY

tj. podanie modelu

y₁=a₁₁x₁ + a₁₂x₂

y₂=a₁₁x₁ + a₂₂x₂

Czy jest to model dobry?

Nie wiem, będę musiał sprawdzić: weryfikacje, modulacje.

Ale uznaje, że ten model jest dobry. Jest to model liniowy. Jest to macierz kwadratowa, lub prostokątna w zależności od ilości WE i WY.

Model Statyczny - nie występuje czas, interesuje mnie obserwacja w danym momencie, jak stany znikną podczas badania, to efekt nas interesuje.

Y=Ax

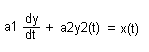
Model dynamiczny - występuje czas, stan aktualny zależy od stanów poprzednich.(np. wzrost produkcji i dynamika wzrostu)

a1,a2 > 0

Przykład : Model matematyczny opisujący prąd przemienny.

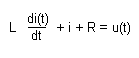
Do opisów modeli dynamicznych zawsze będzie potrzebne równanie różniczkowe

2. Sformułuj zadanie identyfikacji.

IDENTYFIKACJA, ROZPOZNAWANIE

(b. Specyficzna identyfikacja)

y₁ = a₁₁x₁ + a₁₂x₂

y2 = a₂₁x₁ + a₂₂x₂

Mamy nieznane parametry:

a₁₁=? a₁₂=? a₂₁=? a₂₂=?

Algorytm identyfikacji - sposób na wyznaczenie tych parametrów.

Eksperyment:

BIERNY	AKTYWNY
W układzie krwionośnym nie można np. podwyższyć ciśnienia u pacjenta, bo umrze, Można u pacjenta zaobserwować ciśnienie np. dziś i jutro, mam 2 wyniki i je przetwarzam.	Jeżeli sami możemy ustalić, zaplanować wejścia. Wykonuje doświadczenie. Np. Sam ustawiam WE.

Identyfikacje przeprowadzamy w przypadku, kiedy znamy dokładny model systemu.

Przykład:

y₁ = a₁₁x₁ + a₂₁x₂ X_1,X₂ - ilość surowców przerabianych w 2 agregatach

y₂ = a₂₁x₁ + a₂₂x₂ Y₁,Y₂ - ilość produktu i kosztu produkcji

Y = AX

A = YX^-1 - algorytm identyfikacji

A = Ψ (x₁,x₂,y₁,y₂)

_

y = Ø (x, a) zakładam sobie model z dokładnością parametrów

Ilość obserwacji WY zew. obiektu

↓ ↓

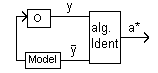
_{n _ n}

Q_I =∑ ( y_i - y_i )² =(mają nie być różne od siebie)= ∑ ( y_{i -} Ø(a₁ x_i ))²

^{i=1 i=1}

^↑

^{WY modelu (wylicze sobie)}

Min Q(a) → a*

^a

Obliczam I pochodną i sprawdzam I lub II warunek wystarczający istnienia min funkcji.

_{_}

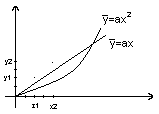
y = ax

_{_}

y = ax² - klasa modeli kwadratowa Obliczanie sumy

odl. od prostej

pomiary i-tego a

_{n n}

Q_I = ∑ (y₁ - Ø(a₁x_i))² = ∑ (y₁ - ax₁)²

^{i=1 i=1}

_{dQ n}

― = ∑ 2(y₁ - ax₁) (-x_i) = 0

^{da i=1}

_n

∑ (ax_i² - x_iy_i) = 0

ⁱ⁼¹

_{n n}

a ∑ x_i² - ∑ x_iy_i = 0

^{i=1 i=1}

_n

∑ x_iy_i Algorytm identyfikacji wygląda dokładnie tak.

ⁱ⁼¹ Model statyczny, liniowy.

a = ------------- Najlepsze rozwiązanie w miare minimalizacji danego kryterium

_n

∑ x_i²

ⁱ⁼¹

3. Opisz zadanie analizy  w sterowaniu systemem.

Analiza (Systemu) ilościowa:

Pytanie: Jak zachowuje się WE, kiedy zmieni się WE?

Dokonuje analizy działania systemu. Jak zachowuje się WY dla różnych WE, tj. zadanie ANALIZY.

W przypadku prostych układów wyliczenie y znając konkretne wartości parametrów.

DEF.

„Jeżeli znamy wartości liczb parametrów a₁₁,a₁₂,a₂₁,a₂₂ to wstawiamy dane x₁,x₂ do modelu i wyliczamy y₁,y₂.”

Analiza jakościowa:

Czy system ma pewne własności np. czy jest stabilny(pewne wielkości nie będą dążyć do nieskończoności).

5. Scharakteryzuj przyczyny właściwości dynamicznych systemów.

Model dynamiczny - występuje czas, stan aktualny zależy od stanów poprzednich.(np. wzrost produkcji i dynamika wzrostu)

a1,a2 > 0

Przykład : Model matematyczny opisujący prąd przemienny.

Do opisów modeli dynamicznych zawsze będzie potrzebne równanie różniczkowe

6. Omów pojęcie stanu układu dynamicznego

Stan systemu dynamicznego :

Jest to najmniejsza liczba danych(wektor stanu), których znajomość danej chwili, przy znajomości wielkości WE, począwszy od tej chwili pozwala jednoznacznie określić stan i wielkości WY systemu w przyszłości.

Zdeterminowanie systemu wynika z postulatów: przyczynowości, zupełności.

Ilość zmiennych stałych, które określają położenie danego

Obiektu jest różna.

1 i 2 wpływa na 3 i 4

Więc systemy są zdeterminowane, znając stan WE można

Obliczyć WY.

Postulat przyczynowości:

Not: Dopóki WE stanu jest takie same, to sterowanie tez takie

same => przyczyna zmiany stanu.

Postulat zupełności:

Not: Zmian jest jednoznaczna w odwrotną stronę. Kiedy WE stanu jest takie same, to sterowanie różne, natomiast jak sterowanie takie same, to WE stanu też

Przykład:

Zbiornik wody - stopień zapełnienia:

Dx(t)

------ = u(t) - y(t)

dt

↑ ↑ ↑

WE WY

prędkość zmiany co wpływa do to co wypłynęło, już

stanu(pochodna) wykonania wypływa

(tutaj woda,

deszcz)

y(y) = y(x(t))

wyznaczam x(t):

_{t t}

x(t) = ∫ u(t)dt - ∫ y(t)dt

• ⁰

Całka oznaczona - suma wielkości, sumowanie przebiegu, który zmienia się w czasie

Całka - sumowanie, czyli uwzględnienie tego , co było po drodze.

8. Omów na przykładzie opis w postaci transmitancji.

Transmisją operatorową:

G(s) liniowym układu (Obiektu) liniowego stacjonarnego nazywać będziemy wartość określoną jako stosunek transformaty wymuszenia U(s) tego układu przy zerowych warunkach początkowych. G(s) =Y(s) / U(s)

9. Omów na przykładzie odpowiedź skokową układu.

Charakterystyką(Odpowiedzią) skokową:

H(t) jednowymiarowego układu (obiektu) liniowego stacjonarnego, nazywać będziemy odpowiedź tego układu na wymuszenie w postaci jednostkowej funkcji skokowej 1(t), przy zerowych warunkach początkowych.

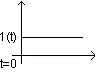
←impuls

10. Omów na przykładzie odpowiedź impulsową układu.

Charakterystyką( Odpowiedzią) Impulsową

G(t)liniowym układu( Obiektu) liniowego, stacjonarnego nazywać będziemy odpowiedź tego układu na wymuszenie w postaci funkcji Diraca (t), przy zerowych warunkach początkowych.

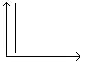
δ(t) ←impuls o nieskończonej amplitudzie, duży impuls,

o dużym czasie trwania.

11. Człon inercyjny

CZŁON INERCYJNY:

(piec)

(Jak funkcja określona w czasie

I - pochodna mówi o prędkości zmian

II - pochodna o przyspieszeniu)

.

Równanie różniczkowe WE/WY: Ty + y = ku

k - współczynnik wzmocnienia określany jako stosunek odpowiedzi y do wymuszenia u w stanie ustalonym.

T - stała czasowa.

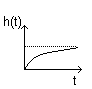
Charakterystyka skokowa:

h(t) = k( 1 - ex [(-1)/T]) 1(t)

Odpowiedź impulsowa:

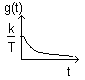
g(t) = K/T ex [(-1)/T] 1(t)

Transmitacja:

k

G_s =

1 + sT

kierunek przepływu prądu

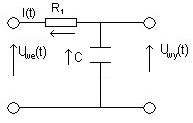
**Przykład 1:

CZWÓRNIK RC

Nieobciążony.

U_we(t) = RI(t) + 1/C ∫ I(t) dt

U_we(t) = RI(t) + U_wy(t)

U_wy(t) = 1/C ∫ I(t) dt

d U_wy(t) 1

= * I(t) tj. funkcja czasu

dt C

RC d U_wy

U_we(t) = . * + U_wy

T y + y dt

Oznacza to, że jak włącze napięcie na WY nie pojawi się niezwłocznie, tylko będzie narastać.

Im stała czasowa mniejsza, tym szybciej zostanie osiągnięty stan przez WY.

**Przykład 2:

ELEMENT GRZEWCZY:

P - moc jest funkcją czasu P(t); energia dostarczana do grzejnika

dt - mały czas (delta t) energia ta rozkłada się na ciepło

dodawane i wydalane

P(t)dt = c*m *d Θ(t) + α
S Θ dt α - stała

S - powierzchnia grzejnika

Θ - ilość ciepła proporcjonalna do

To co się kumuluje to co się rozprasza temp, zmienia się w czasie

w grzejniku

Mamy bilans cieplny:

P(t)dt = c*m*d Θ(t) + αS*Θ(t) dt

1 c*m d*Θ(t) .

* P(t) = * + Θ(t) k*u(t) = T * y + y

α*S α * S dt

**Przykład 3:

GENERATOR

PRĄDU STAŁEGO

Nieobciążony

I_u(t) - prąd wzbudzenia

d*I*w(t)

L + R*I*w(t) = Uw(t)

dt

d*E(t) d*I(t)

= K

dt dt

L d*e(t) R

* + E(t) = Uw(t)

K dt K

Podsumowanie:

Co uzyskujemy?

Układy o różnych naturach podlegają pod te same równania jak odrzuce skale i jednostkę MATEMATYKA jest wszędzie.

12. Człon całkujący z inercją,

CZŁON CAŁKUJĄCY Z INERCJĄ

.. .

Równanie różniczkowe WE - WY: Ty + y = ku

K - współczynnik wzmocnienia prędkościowego określany jako stosunek pochodnej odpowiedzi y do wymuszenia u w stanie ustalonym

T - stała czasowa

Charakterystyka skokowa:

t

h(t) = (kt - kT ( 1-exp [- ] ) ) 1(t) układ będzie dążył do całki

idealnej.

T

Odpowiedź impulsowa:

t

h(t) = k [ 1-exp [- ] ] 1(t)

T

K

Transmitacja: g(s) =

S(1+sT)

Przykłady:

1. OBCOWZBUDNY SILNIK PRĄDU STAŁEGO

Założenia: silnik nieobciążony, uwzględniamy tylko bezwładność

We - napięcie twornika

Wy - kąt położenia wału silnika

Ω(t) (WY - położenie kątowe)

α(t)

Ø - strumień jednego z uzwojeń

Const

DI(t)

U(t) = R_t * I(t) + L_t E(t)

dt

pomijam(małe)

dΩ(t)

M_n(t) - M_z(t) = I M_n(t) = C_m * Ø * I(t)

dt

Chcemy powiązać 2 wielkości: α(t) i U(t)

d α(t)

= Ω(t) No i manipulujemy, aby była zależność α(t) do U(t)

dt

dΩ(t)

C_m Ø Ω(t) * I(t) = J

dt

U(t) = R_t * I(t) + C_E Ø Ω(t)

J dΩ(t)

I(t) = *

C_M Ø dt

R_t * J d² α dα

U(t) = * + C_EØ

C_mØ dt² dt

13. Człon różniczkujący z inercją

CZŁON RÓŻNICZKUJĄCY Z INERCJĄ

(rzeczywisty człon różniczkujący)

. .

Równanie różniczkujące WE-WY: Ty + y = ku

K - współczynnik wzmocnienia określany jako odpowiedź y do pochodnej wymuszenia u w stanie ustalonym

T - stała czasowa

k 1

Charakterystyka skokowa: h(t)= exp ( - ) 1(t)

T T

Odpowiedź impulsowa: k k 1

g(t)= δ(t) - exp( - ) 1(t)

T T² T

ks

Transmitacja: g(s) =

1+sT

Przykład:

CZWÓRNIK R,L d I(t)

U_we(t) = R * I(t) + L =

dt

= R I(t) + U_wy(t)

dI(t)

U_wy(t) = L

dt

d U_we(t) d I(t) d U_wy(t)

= R +

dt dt dt

Równanie końcowe:

d U_we R d U_wy . _.

= * U_wy(t) + => u = k * y + y

dt L dt

Przykład **:

TRANSFORMATOR :

d I₁

U₁ = RI₁ + L₁

dt .

I

d I₁

U₂ = M

dt

. . ..

U₁ = R₁ I₁ + L₁ I

. R L₁ .

U₁ = U₂ + U₂ / M/R

M M

M . L₁ .

U₁ = U₂ + U₂

R R₁

K T

14. Człon oscylacyjny,

CZŁON OSCYLACYJNY

Odpowiada na wymuszenie

1. Tłumione

2.Nie Tłumione

3. Narastanie.

DOPISAC PRZYKŁAD

15. Człon opóźniający

CZŁON OPÓŹNIAJĄCY

Równanie różniczkowe: y(t) = ku( t - T₀)

K - współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia u dla

t >T₀

T₀ - czas opóźnienia

Charakterystyka skokowa: h(t) = k 1(t - T₀)

Odpowiedź impulsowa: g(t) = kδ(t - T₀)

Transmitacja: g(s) = ex (-sT₀)

---