1. Wypływa cieczy ze zbiornika.

Opis aparatury:

Ćwiczenie składa się z dwóch statywów, na których są umieszczone dwie butelki. Jedna z nich ma przekrój poprzeczny jednakowy na całej długości tzn. jest prostopadłościanem, a druga ma przekrój zmienny, tzn. w jednej z części jest walcem, a w drugiej stożkiem. Butelki są umocowane spodem do góry. Dna w tych butelkach są usunięte. W nakrętkach butelek są zrobione małe otwory, mające na celu umożliwienie wypływu cieczy. Zastosowany zbiorniki to butelka o jednakowym przekroju poprzecznym (kwadrat o boku 9cm) z otworem w nakrętce o średnicy 3mm (Rys. 1) oraz butelka o zmiennym przekroju: walca o podstawie koła o promieniu r = 4,5cm oraz stożka i otworze w nakrętce o średnicy 3mm (Rys. 2).

Wykonanie ćwiczenia:

Zatykając otwory w nakrętkach butelek nalewamy wodę, tak, by nalać do nich pełny litr. Następnie odtykając otwory w nakrętkach mierzymy czas stoperem wypływu cieczy aż do opróżnienia zbiornika.

Rys. 1. Butelka pomiarowa 1.

Rys. 2. Butelka pomiarowa 2.

Poniższa tabela przedstawia wyniki pomiarów:

Tabela 1. Wyniki pomiarów wypływu cieczy

Lp.	τ [s] (butelka walcowa- przekrój stały)	τ [s] (butelka stożkowa- przekrój zmienny)
1.	68	118
2.	69	119
3.	67	117

Pomiar wykonaliśmy trzykrotnie, gdyż rozbieżności pomiędzy wynikami nie wynosiły więcej niż 5%.

Wyznaczenie współczynnika wypływu otworu w dnie dla obu zbiorników:

Zbiornik I

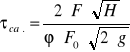
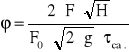
Dane:

g ≈ 9,81 m/s²

F= 9,00²=81 cm²

H=21,5 cm=0,215m

Obliczenia:

τ_cał.= (68s+69s+67s)/3=68 s

fi = (2 * F * *H) / (F₀*(*2g)* τ_cał.)

fi = 2*81**0,215/(0,0706*(*2*9,81)* 68)

fi = 3,53

Dyskusja jednostek:

Stwierdzono, że wyliczona wartość jest bezwymiarowa.

Zbiornik II

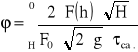
Dane:

g ≈ 9,81 m/s²

d= 9 cm

H₁=14 cm= 0,14m

H₂=9cm= 0,16 m

Obliczenia:

H= H₁ + H₂=0,14m +0,16 m= 0,3 m

118+119+117/3= 118

Tcał= 118+119+117/3= 118

fi = 2*117*pierwiastek(0,23)/(0,0706*PIERWIASTEK(2*9,81)*183,12)= 1,95

Dyskusja jednostek:

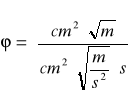
Stwierdzono, że wyliczona wartość jest bezwymiarowa.

Wyznaczenie błędów pomiarów.

Błędy niedokładnego pomiaru czasu opróżnienie zbiornika wynikają z niesynchronizowania włączenia stopera a odetkania otworu. A także zanieczyszczeniami zawartymi na powierzchni butelki lub znajdującymi się w wodzie.

Niedokładny pomiar wymiarów zbiornika spowodowany jest tym, że butelka nie była idealnym prostopadłościanem ani stożkiem i walcem. Butelka ta posiadała liczne wgłębienia, których nie uwzględnialiśmy w pomiarach. Błąd może być również spowodowany wykonywaniem pomiarów linijką, która jest niedokładnym urządzeniem pomiarowym.

Wyznaczenie błędu bezwzględnego i względnego pomiaru współczynnika wypływu otworu w dnie dla obu zbiorników.

Błąd bezwzględny:

Zbiornik I

Zbiornik II

Błąd względny:

Zbiornik I:

Zbiornik II:

Wartość ciśnienia działającego na powierzchnię lustra cieczy.

Zbiornik I

Dane:

H = 20cm=0,2m

g ≈ 9,81 m/s²

ρ = 1000 kg/m³

Obliczenia:

Zbiornik II

Dane:

H = 24,5cm=0,245m

g ≈ 9,81 m/s²

ρ = 1000 kg/m³

Obliczenia:

Dyskusja jednostek:

Współczynnik wypływu jest zależny od gęstości cieczy wypływającej( im większa gęstość tym większy współczynnik) oraz od wielkości otworu odpływowego. Na przykład biorąc pod uwagę wodę i oliwę, ich gęstości są różne. Oliwa ma większą wartości gęstości niż woda, więc jej czas wypływu ze zbiornika będzie dłuższy niż czas wypływu wody, zatem gęstość cieczy jest zależna od czasu opróżniania zbiornika.

Całkowity czas wypływu ze zbiornika prostopadłościennego pionowego:

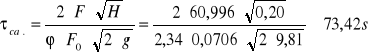
s

Wnioski:

Współczynnik wypływu otworu w dnie zbiornika I wyniósł 2,34 natomiast współczynnik wypływu otworu w dnie zbiornika II wyniósł 0,32. Współczynnik ten jest zależny od gęstości wypływającej cieczy (im większa gęstość tym większy jest współczynnik). Zależy on również od wielkości otworu odpływowego. Wartość ciśnienia działającego na powierzchnię lustra wody wyniosła dla pierwszego zbiornika wyniosła:  -1962Pa, a dla drugiego zbiornika: -2403Pa (podciśnienie).Wartości te mogły być obarczone błędami spowodowanymi złymi pomiarami zbiornika (szczególnie otworu), ponieważ nie używamy profesjonalnych przyrządów pomiarowych tylko linijki, która mogła wykazać złą wartość. Błędy mogą wynikać również z niedokładności pomiaru czasu wypływu wody ze zbiorników.

2. Badanie oporów przepływów.

Cel ćwiczenia:

Celem ćwiczenia było wyznaczenie charakteru przepływu cieczy nieściśliwej w poszczególnych odcinkach przewodu, oraz oporów liniowych i miejscowych jej przepływu.

Opis aparatury:

Aparatura zbudowano z otwartego zbiornika na wodę, z którego wyprowadzony został zespół kanałów przepływowych (rys. 1, rys. 2,rys. 3) składających się z rurek o średnicy ½”, kolanek i trójnika o tej samej średnicy, oraz rozszerzenia o średnicy ¾”.

Rys. 3. Schemat układu przepływu - rzut izometryczny

Rys. 4. Schemat układu przepływu - rzut z przodu

Rys. 5. - Schemat układu przepływu - widok z boku

Przebieg ćwiczenia:

Początkowym pomiarem, było wyznaczenie temperatury i ciśnienia powietrza w laboratorium. Temperatura wody w zbiorniku, zgodnie ze wskazaniem prowadzącego, została przyjęta jako temperatura otoczenia.

Wypływ cieczy ze zbiornika następował po otwarciu zaworu głównego, oraz jednego lub dwóch zaworów wylotowych. Ustalenie warunków układu następowało po odkręceniu wszystkich zaworów, do momentu wypływu cieczy z obydwu wylotów. Następnie zakręcono zawory wylotowe i poczekano do momentu ustalenia się poziomu cieczy w zbiorniku.

Objętość cieczy, która opuściła układ przepływu wyznaczono za pomocą wyskalowanego pojemnika. Czas przepływu cieczy zmierzono przy użyciu stopera. Ubytek cieczy w zbiorniku głównym uzupełniano wodą zebraną do naczynia pomiarowego po każdorazowym pomiarze. Każda seria pomiarów składała się z pięciu powtórzeń, co umożliwia wyeliminowanie błędów pomiarowych grubych.

Wyniki pomiarów dla pierwszej serii pomiarów - wypływ cieczy po otwarciu jednego zaworu wylotowego przedstawia Tabela 1.

Tabela 2. Wyniki pomiarów dla pierwszej serii pomiarów - wypływ cieczy po otwarciu jednego zaworu wylotowego

Lp.	Czas [s]	Objętość cieczy [ml]
1	17,48	630
2	19,57	630
3	21,74	700
4	22,4	710
5	18,87	630

Wyniki pomiarów dla drugej serii pomiarów - wypływ cieczy po otwarciu dwóch zaworów wylotowych przedstawia Tabela 2.

Tabela 3. Wyniki pomiarów dla drugej serii pomiarów - wypływ cieczy po otwarciu dwóch zaworów wylotowych

Lp.	Czas [s]	Kanał wylotowy lewy [ml]	Kanał wylotowy prawy [ml]
1	16,54	780	50
2	24,11	650	300
3	18,56	470	290
4	24,33	640	360
5	25,15	880	120
6	18,83	500	300

Temperatura wody wynosi 21,2°C, ciśnienie powietrza 1006hPa.

Obliczenia dla pierwszej serii pomiarowej.

Równanie Bernoullego, przedstawiające charakterystykę przepływu w układzie: :

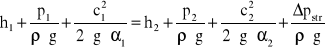
,gdzie:

h₁ = 100mm = 0,1m - wysokość słupa cieczy w zbiorniku,

h₂ ≈ 0,

p₁ = p₂, przyjęto równe ciśnienia dla zbiornika i układu przepływu,

c₁ ≈ 0, prędkość przepływu wody w zbiorniku.

c2 - średnia prędkość przepływu wody w układzie.

Kanał przepływowy składał się z odcinków o następujących długościach:

l₁=280mm = 0,28m,

l₂=230mm = 0,23m,

l₃=310mm = 0,31m,

l₄=145mm = 0,145m,

l₅=1025mm = 1,025m - odcinek o średnicy ¾”,

l₆=535mm = 0,535m,

l₇=160mm = 0,16m,

l₈=305mm = 0,305m,

l₉=1495mm = 1,495m,

l₁₀=670mm = 0,67m.

długość całkowita rur o średnicy ½” Δl₁=4,13m, a o średnicy ¾” Δl₂=1,025m

Wyznaczenie c₂ dla pierwszej serii pomiarowej jako średniej arytmetycznej z prędkości dla kolejnych pomiarów.

Należy uwzględnić, że przy przepływie z otwartym jednym zaworem wylotowym udział długości rurki o średnicy ¾” w stosunku do całkowitej długości kanału przepływowego wynosi w przybliżeniu 20%. Wraz ze zmianą powierzchni przekroju rurki, zmienia się prędkość przepływu. Prędkość przepływu przez szerszy kanał wyznaczono z równania stałości przepływu:

c_2a * F1 = c_2b * F2

, czyli

,

c_2a jest średnią arytmetyczną z prędkości przepływów wyznaczonych w kolejnych pomiarach:

i ostatecznie

c_2a = 0,26 m/s,

więc:

c_2b = 0,15 m/s,

Wyznaczenie charakteru przepływu.

Charakter przepływu opisuje liczba charakterystyczna Reinoldsa Re, wyznaczona zgodnie z tablicą 8.

gdzie:

c2 - średnia prędkość przepływu cieczy,

d - srednica wewnętrzna kanału,

ν - współczynnik lepkości kinematycznej płynu, odczytany z tabeli 18 dla t=20°C, czyli temperatury wody; ν=1,006 * 10^-6 [m²/s]

, czyli:

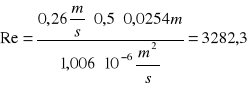
Dla wskazanych danych liczba Reinoldsa wynosi:

,

co oznacza, że przepływ ma charakter burzliwy.

Natomiast dla przekroju grubszego:

Dla wskazanych danych liczba Reinoldsa wynosi:

,

co oznacza, że przepływ jest w dalszym ciągu burzliwy.

Następnie wyznaczono empiryczny współczynnik liniowych oporów przepływu z tablicy 5

,

Gdzie współczynniki a, b, n przyjęto z równania Blassiusa:

a=0, b=0,3164, n=0,25

Po podstawieniu do wzoru otrzymano wartość współczynnika λ dla wąskiej rurki:

oraz dla szerokiej:

Otrzymaną wartość współczynnika wstawiono do wzoru Darcy'ego-Weisbacha opisującego liniowe opory przepływu:

długość całkowita rur o średnicy ½” Δl₁=4,13m, a o średnicy ¾” Δl₂=1,025m, więc:

dla rur o średnicy ½”:

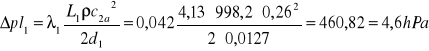
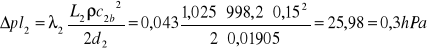
, czyli łącznie:

Liczba Reynoldsa zmienia się w zależności od średnicy rurki, toteż w rurce o średnicy ¾” jest ona większa, jednak nie zmienia to charakteru przepływu, który pozostaje burzliwy.

Wyznaczenie oporów miejscowych.

Zmiana przekroju i kierunku przepływu powoduje zawirowania strumienia, co z kolei generuje straty energii płynu, a w efekcie straty ciśnienie. Opory te nazywa się oporami miejscowymi, które opisuje wzór:

gdzie:

ρ - gęstość cieczy

c - średnia prędkość przepływu

ξ - Współczynnik oporów miejscowych

Wartość ξ zależy tylko od kształtu elementów na których występują zawirowania

Z tablicy 6 odczytano współczynniki oporów miejscowych ξ dla kolejnych elementów:

ξ₁ = 0,5, ξ ₂ = 1,1, ξ ₃ = 1,1, ξ ₄ = 1,1, ξ ₅ = 0,118, ξ ₆ = 0,22, ξ ₇ = 0,14, ξ ₈ = 1,1, ξ ₉ = 1,1, ξ ₁₀ = 1

Σ ξ = ξ₁ + ξ ₂ + ξ ₃ + ξ ₄ + ξ ₅ + ξ ₆ + ξ ₇ + ξ ₈ + ξ ₉ + ξ ₁₀

Σ ξ = 7,478

Wartości współczynników miejscowych oporów odczytane zostały z tablicy 6.

Ciecz przepływając przez kanał o zmiennym przekroju oraz zmiennym kierunku przepływu (kolanka lub rozdzielacze), pokonuje również miejscowe opory przepływu:

na wlocie przewodu ξ₁ = 0,5

,

na pierwszym kolanku, ξ ₂ = 1,1

na drugim kolanku, ξ ₃ = 1,1

na trzecim kolanku, ξ ₄ = 1,1

na nagłym rozszerzeniu, ξ ₅ = 0,118, ponieważ:

, stąd przy wykorzystaniu interpolacji liniowej wyznaczono ξ₅:

, czyli:

na nagłym zwężeniu ξ ₆ = 0,22, ponieważ:

, czyli

Na łagodnym kolanku, ξ ₇ = 0,14

, ponieważ promień zaokrąglenia R > 3d

na czwartym kolanku, ξ ₈ = 1,1

na piątym kolanku, ξ ₉ = 1,1

na szóstym kolanku, ξ ₁₀ = 1,1

na wylocie, ξ ₁₁ = 1

,

Sumaryczny spadek ciśnienia podczas przepływu przez kanał wyraża się wzorem:

,

Δp_m = 2,81 hPa.

Dla przepływu burzliwego przyjęto α=1 oraz g=10 m/s², ρ=998,2 kg/m³

Wyznaczenie sumarycznych oporów przepływu.

Sumaryczne spadek ciśnienia wywołany oporami przepływu wyraża się wzorem:

Obliczenia dla drugiej serii pomiarowej.

Wyznaczenie oporów przepływów przy otwartych wszystkich zaworach.

Analogicznie do wcześniejszych obliczeń, wyznaczono średnią prędkość przepływu dla drugiej serii pomiarowej. Zmianie uległa prędkość przepływu, długość kanału o średnicy ½” oraz opory liniowe i miejscowe (spowodowane zamianą kolanka na trójnik) i odpowiednio wynoszą:

C_2a=0,33 m/s

C_2b-0,15 m/s

Δl₁=6,295m,

ponieważ wydłużono kanał o następujące odcinki:l₉= 1,495m oraz l₁₀= 0,67m.

Charakter przepływu jest ciągle burzliwy, ponieważ w stosunku do pierwszej serii pomiarowej zwiększa się średnia prędkość przepływu, czyli zwiększa się też liczba Reynoldsa.

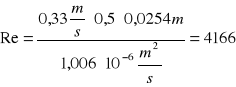
Re = 4166

A dla przepływu przez rurkę szerszą:

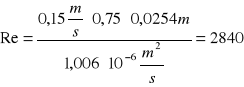
Re = 2840

Następnie wyznaczono empiryczny współczynnik liniowych oporów przepływu z tablicy 5

,

Gdzie współczynniki a, b, n przyjęto z równania Blassiusa:

a=0, b=0,3164, n=0,25

Po podstawieniu do wzoru otrzymano wartość współczynnika λ dla wąskiej rurki:

oraz dla szerokiej:

Dla przepływu burzliwego przyjęto ponownie α=1 oraz g=10 m/s², ρ=998,2 kg/m³

Ponownie wyznaczono opory liniowe:

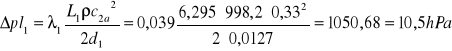
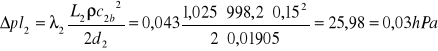
, czyli łącznie:

Wyznaczenie oporów miejscowych:

na wlocie przewodu ξ₁ = 0,5

,

na pierwszym kolanku, ξ ₂ = 1,1

na drugim kolanku, ξ ₃ = 1,1

na trzecim kolanku, ξ ₄ = 1,1

na nagłym rozszerzeniu, ξ ₅ = 0,118, ponieważ:

, stąd przy wykorzystaniu interpolacji liniowej wyznaczono ξ₅:

, czyli:

na nagłym zwężeniu ξ ₆ = 0,22, ponieważ:

, czyli

Na łagodnym kolanku, ξ ₇ = 0,14

, ponieważ promień zaokrąglenia R > 3d

na trójniku ξ ₈ = 2

na piątym kolanku (są teraz dwa symetrycznie rozmieszczone), ξ ₉ = 1,1

lecz po trójniku ciecz wypływa dwoma kanałami z dwiema prędkościami przepływu

c_{2a lewy}=0,248 m/s = 0,25 m/s

c_{2a lewy}=0,088m/s = 0,09 m/s

na szóstym kolanku (są teraz dwa symetrycznie rozmieszczone),, ξ ₁₀ = 1,1

na wylocie (są teraz dwa symetrycznie rozmieszczone), ξ ₁₁ = 1

Sumaryczny spadek ciśnienia podczas przepływu przez kanał wyraża się wzorem:

,

Δp_m = 4,29 hPa.

Sumaryczny spadek ciśnienia wywołany oporami przepływu wyraża się wzorem:

Procentowy wzrost spadku ciśnienia wynosi zatem:

Δ(Δp)

Wnioski.

Przepływ cieczy nieściśliwej przez różne przekroje oraz załamania w postaci kolanek i rozdzielaczy może powodować zmianę prędkości przepływu a nawet charakteru przepływu z burzliwego na laminarny i odwrotnie. Lepkość cieczy powoduje tarcie o ścianki przewodu, co znacząco wpływa na sposób przemieszczania się cieczy i rozkład jej prędkości. Zwiększenie chropowatości powierzchni rurki wydatnie zmniejsza prędkość przepływu przy ściankach (Rys. 6).

Rys. 6. Rozkład prędkości cieczy w rurce.

Przy dużej lepkości i bardzo nierównomiernym kanale przepływowym opory ruchu mogą być duże, że znacząco wpływają na obciążenie pompy tłoczącej czynnik. Spadek ciśnienia w kanale jest uzależniony od jego długości, średnicy i chropowatości zastosowanych powierzchni wewnętrznych rurek, charakteru załamań i zmian przekroju kanału oraz rodzaju zastosowanej cieczy. Jak pokazało doświadczenie, zwiększenie długości kanału zbudowanego z rurek o średnicy ½” o ok. 34% i zastosowanie trójnika spowodowało wzrost spadku ciśnienia o 48%.

W doświadczeniach zastosowano niedokładne przyrządy pomiarowe - pojemnik z niewystarczającą rozdzielczością podziałki oraz pomiar czasu przepływu przy wykorzystaniu stopera, co uniemożliwia idealną koordynację jego startowania i zatrzymywania wraz z rozpoczęciem i zakończeniem przepływu cieczy. Nie można zakładać, że zamknięcie zaworów wylotowych w drugiej serii pomiarowej zostało idealnie skoordynowane. W rzeczywistości jest bardzo prawdopodobne, że zawory nie zostały całkowicie otwarte lub zamknięte. Zakłócenia w przepływie mogły zostać także spowodowane zanieczyszczeniami czynnika roboczego, ponieważ w układnie nie zastosowano dokładnego systemu filtracji (zamontowano tylko siatkę o duże średnicy oczek)

Wszystkie powyższe czynniki wpływają niekorzystnie na jakość odczytów z serii pomiarowych, co z kolei uniemożliwiło wyznaczenie spadków ciśnienia z wysoką dokładnością.

Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 148.

Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 215.

Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 196..

Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 196

Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 196.

Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 196.

---