Nr ćwiczenia
201 |
Data
17.11.2000 |
|
Wydział Budownictwa, Architektury i Inżynierii Środowiska |
Semestr I
|
Grupa 13 Nr lab. 3 |
|
Przygotowanie |
Wykonanie |
Ocena |
||
Temat: Wyznaczanie zależności przewodnictwa od temperatury dla przewodników i półprzewodników.
Prawo Ohma w najogólniejszej postaci stwierdza, że gęstość prądu w dowolnym miejscu materiału przewodzącego jest wprost proporcjonalna do natężenia pola elektrycznego.
j = σE
W powyższym równaniu j oznacza gęstość prądu (stosunek prądu do powierzchni przekroju), natomiast E natężenie pola elektrycznego. Współczynnik proporcjonalności σ nazywamy przewodnictwem elektrycznym. Wartość przewodnictwa określona jest bezpośrednio przez koncentrację i ruchliwość nośników ładunku. Przewodnictwo elektryczne określone jest wzorem :
![]()
n , p - koncentracje nośników ,
n , p - ruchliwość nośników .
Ponieważ koncentracja i ruchliwość zależą od temperatury i rodzaju materiału , więc przewodnictwo elektryczne także zależy od tych czynników .
O zależności temperaturowej przewodnictwa w metalach decyduje tylko zmniejszanie się ruchliwości wraz ze wzrostem temperatury ( koncentracja nośników - elektronów - jest bardzo duża i nie zależy od temperatury ) . Zależność temperaturową wyraża się poprzez opór (R1/ ) :
![]()
,
R0 - opór w temperaturze T0 ,
- średni współczynnik temperaturowy oporu
W półprzewodnikach decydujący wpływ na przewodnictwo ma koncentracja nośników. W przypadku półprzewodników samoistnych koncentracja elektronów i dziur jest taka sama i wynosi :
![]()
,
Eg - szerokość pasma zabronionego .
Natomiast w półprzewodnikach domieszkowych koncentracje określone są poprzez poziomy energetyczne (zależnie od typu półprzewodnika ) Ed - donorowy , Ea - akceptorowy , oraz poprzez temperaturę :
![]()
.
Uwzględniając powyższe równania otrzymujemy wzór na temperaturową zależność przewodnictwa dla półprzewodników :
![]()
,
Edom jest jedną z wielkości Ed lub Ea zależnie od typu półprzewodnika .
W odpowiednio niskich temperaturach można zaniedbać w powyższym wzorze pierwszy składnik , natomiast w wysokich temperaturach ( po nasyceniu poziomów domieszkowych ) można zaniedbać składnik drugi . Odpowiednio dla tych dwóch przypadków wzór przyjmie postać :
![]()
.
Logarytmując jeden z powyższych wzorów otrzymamy zależność :
![]()
Pomiarów oporu półprzewodnika i przewodnika dokonuje się w różnych temperaturach . Badane materiały umieszczone są w ultratermostacie , a ich opory mierzy się przy pomocy mostka Wheatstone'a.
Z wykresu tej zależności wygodnie jest odczytać zależność przewodnictwa od temperatury
PRZEBIEG ĆWICZENIA
Znaleźć przybliżoną wartość oporów w temperaturze pokojowej.
Włączyć do sieci ultratermostat, dołączyć baterie, galwanometr i oporniki badane do mostka Wheatstone'a.
Ustalić temperaturę 20˚C w ultratermostacie włączając, w zależności od potrzeby, chłodnicę lub grzejnik.
Dokonać pomiaru oporów przewodnika i półprzewodnika.
Zmieniać temperaturę co ok. 5˚C w zakresie 20 - 90˚C i mierzyć opory.
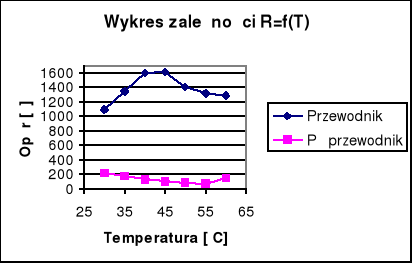
Wykreślić zależność R = f(T) na wspólnym wykresie dla przewodnika i półprzewodnika.
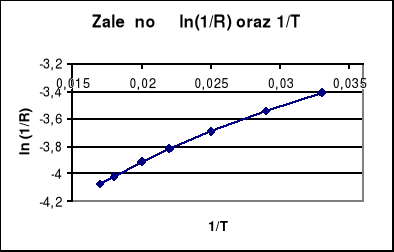
Dla półprzewodnika obliczyć ln (l/R) oraz l/T i sporządzić wykres zależności tych wielkości.
Z nachylenia wykresu obliczyć położenie poziomu domieszkowego. Położenie poziomu domieszkowego wyrazić w elektronowoltach.
TABELA POMIARÓW
l.p. |
T [˚C] |
Opór przewodnika [Ω] |
Opór półprzewodnika [Ω] |
1 |
30 |
1100 |
220 |
2 |
35 |
1342 |
180 |
3 |
40 |
1590 |
140 |
4 |
45 |
1606 |
110 |
5 |
50 |
1403 |
83 |
6 |
55 |
1316 |
71 |
7 |
60 |
1290 |
150 |
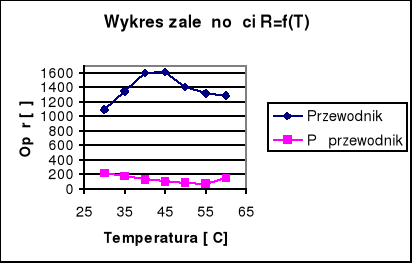
OBLICZENIA
(tylko dla półprzewodnika)
L.p.
|
T [C] |
1/T [1/C] |
R [] |
1/R [1/] |
ln(1/R)
|
1 |
30 |
0,033 |
220 |
0,004545 |
-5,393628 |
2 |
35 |
0,029 |
180 |
0,005556 |
-5,192957 |
3 |
40 |
0.025 |
140 |
0,007143 |
-4,941642 |
4 |
45 |
0,022 |
110 |
0,009091 |
-4,70048 |
5 |
50 |
0,020 |
83 |
0,012048 |
-4,418841 |
6 |
55 |
0,018 |
71 |
0,014085 |
-4,26268 |
7 |
60 |
0,017 |
150 |
0,006667 |
-5,010635 |
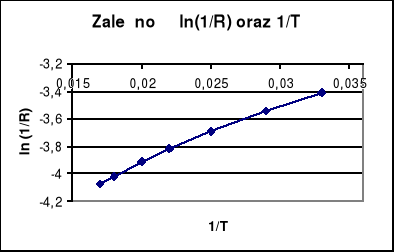
Pomiar nr 7 odrzuciłem. Jest to błąd gruby.
Współczynnik nachylenia prostej ln(1/R)=f(1/T) obliczony programem p. Szuby wynosi:
a = -52,96
Poziom domieszkowy będzie zatem równy:
a = ![]()
E = ![]()
k - stała Boltzmanna
E = ![]()
1,46239719![]()
J
1J = ![]()
E = 0,012307489 eV
Błąd pomiaru rezystancji mostkiem Wheatstone'a : R=0.1
Błąd pomiaru temperatury : T=0.5C
Wyszukiwarka
Podobne podstrony:
Wyznaczanie zależności przewodnictwa od temperatury, AGA, Nr ćw.
Wyznaczanie zależności przewodnictwa od temperatury, F LAB201, Nr ćw.
Wyznaczanie zależności przewodnictwa od temperatury, FIZA201 , Laboratoriu z fizyki
Wyznaczanie zależności przewodnictwa od temperatury, 201z, Laboratoriu z fizyki
201 Wyznaczanie zależności przewodnictwa od temperatury dla półprzewodników i przewodników
Sprawozdanie 1 Wyznaczanie zależności przewodnictwa od temperatury dla półprzewodników i p
Wyznaczanie zależności przewodnictwa od temperatury dla półprzewodników sprawko
spraw, LAB 44, Wyznaczenie zależności rezystancji od temperatury dla metalu i półprzewodnika
spraw, CW44, Wyznaczenie zależności rezystancji od temperatury dla metalu i półprzewodnika
201 3, Wyznaczanie zale˙no˙ci przewodnictwa od temperatury
spraw, SPRAW44, Wyznaczenie zależności rezystancji od temperatury dla metalu i półprzewodnika
Wyznaczenie zależności rezystancji od temperatury dla metalu i półprzewodnika, CEL ˙WICZENIA:
lab 1 - wyznaczanie współczynnika lepkości dynamicznej, zależność lepkości od temperatury, kiciaqq
,Laboratorium podstaw fizyki,?danie zależności rezystancji od temperatury dla metali i półprzewodnik
BADANIE ZALEŻNOŚCI REZYSTANCJI OD TEMPERATURY DLA METALI I PÓŁPRZEWODNIKÓW 3
Badanie zależności rezystancji od temperatury dla metali i półprzewodników 1, 1
więcej podobnych podstron