Politechnika Śląska

Wydział AEiI

Kierunek AiR

Ćwiczenia laboratoryjne z fizyki :

Dyfrakcja światła: wyznaczanie stałej siatki dyfrakcyjnej, pomiar długości światła laserowego, wyznaczanie szerokości szczeliny

Grupa I, sekcja 5

Lesław Kaczor

Jarosław Olczyk

Gliwice 13.04.19941.Opis teoretyczny.

Dyfrakcja jest to zjawisko polegające na uginaniu się promieni świetlnych przechodzących w pobliżu przeszkody, takiej jak np. brzeg szczeliny. Zwykle efekty dyfrakcyjne są małe i trzeba ich uważnie szukać. Poza tym większość żródeł światła to przedmioty rozciągłe, wobec czego obraz dyfrakcyjny wytworzony przez jeden punkt źródła nakłada się na obrazy wytworzone przez inne punkty. Wreszcie, zwykłe żródła światła nie są monochromatyczne. Obrazy dla różnych długości fali nakładają się na siebie i znów zjawisko jest mniej widoczne. Zjawisko dyfrakcji można zaobserwować przy przejściu światła przez wąskie szczeliny lub przeszkody, których szerokość jest rzędu setnych części milimetra. Na ekranie ustawionym za tą szczeliną obserwujemy smugę świetlną otoczoną symetrycznie szeregiem jasnych i ciemnych prążków, stanowiącą obraz dyfrakcyjny szczeliny. Powstanie obrazu dyfrakcyjnego, niezgodne z zasadą prostoliniowego rozchodzenia się promieni, można wyjaśnić na podstawie falowej natury światła. Zgodnie z zasadą Huygensa każdy punkt, do którego dochodzą fale, staje się źródłem elementarnych fal kulistych rozchodzących się wokół tego punktu. Fale te interferując ze sobą stają się przyczyną powstawania jasnych i ciemnych prążków. Praktycznie zazwyczaj nie używa się pojedynczej szczeliny lecz siatki dyfrakcyjnej. Jest to najczęściej płaska płytka szklana pokryta równoległymi rowkami, naciętymi w bardzo małych odległościach. Rysy płytki odgrywają rolę przesłon, natomiast przerwy między nimi rolę szczelin przepuszczających światło.

2.Opis ćwiczenia.

W ćwiczeniu obserwowaliśmy dyfrakcję na siatce dyfrakcyjnej oraz na pojedynczej szczelinie.

1.W pierwszej części ćwiczenia obserwowaliśmy obraz dyfrakcyjny uzyskany przy pomocy siatki dyfrakcyjnej. Siatka była umieszczona w spektrometrze i oświetlona światłem o znanej długości. Należało zmierzyć kąty ugięcia dla trzech rzędów w prawo i w lewo aby na podstawie tych danych i wzoru:

gdzie n -rząd prążka dyfrakcyjnego

wyznaczyć stałą siatki. Pomiar trzeciego rzędu w prawo był utrudniony ze względu na odblaski powstałe na siatce, wobec czego nie został przeprowadzony aby nie wprowadzać błędów do pomiarów. Zamiast kąta trzeciego rzędu został zmierzony czwarty i osobno ujęty w obliczeniach.

2.Druga część ćwiczenia polegała na pomiarze długości światła laserowego, która to wartość jest potrzebna do trzeciej części ćwiczenia. W celu pomiaru długości światła laserowego należało umieścić siatkę dyfrakcyjną o stałej wyznaczonej w ćwiczeniu pierwszym następnie została zmierzona odległość siatki od ekranu oraz położenia kolejnych prążków dyfrakcyjnych na prawo i lewo. Następnie została wyliczona długość światła laserowego ze wzoru:

3. Trzecia część ćwiczenia polegała na wyznaczeniu szerokości szczeliny na której ulegało ugięciu światło laserowe o długości wyliczonej w drugim ćwiczeniu. Pomiar obrazu dyfrakcyjnego był przeprowadzony metodą fotoelektryczną, pomiary były dokonywane co 0.083 mm co zapewnia dokładne odczytanie pozycji kolejnych minimum obrazu dyfrakcyjnego. Następnie została obliczona szerokość szczeliny ze wzoru warunku minimum :

więc :

czyli: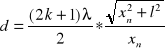

3.Tabela pomiarowa.

Tabela pomiarowa nr. 1

Pomiary kątów ugięcia na siatce dyfrakcyjnej

a0 = 179°40'

Błąd pomiaru Da = 10'

Lp.	n=1		n=2				n=3		n=4
	a1l'	a1p		a2l	a2p	a3l		a4p
1	186°20'	173°40'		193°00'	167°50'	200°20'		152°30'
2	186°20'	173°40'		193°00'	167°50'	200°00'		152°40'
3	186°00'	173°10'		193°00'	167°40'	200°00'		152°20'
4	186°00'	173°40'		193°00'	166°40'	200°00'		152°10'
5	186°00'	173°30'		193°00'	167°00'	200°00'		152°00'

Tabela pomiarowa nr. 2

Pomiary odchyleń światła laserowego na siatce dyfrakcyjnej.

Odległość od ekranu l = 125 cm

Ze względu na rozmycie plamki na ekranie oraz ręczny pomiar odchyleń dokładność pomiaru nie jest większa niż 5 mm.

n	x [cm] (lewo)	x [cm] (prawo)
1	15.5	15.5
2	32.5	32.7
3	-	49.5

4.Opracowanie wyników pomiarów.

1. Wyznaczanie stałej siatki dyfrakcyjnej.

Obliczanie średnich kątów ugięcia. Najpierw zostały obliczone średnie wartości kątów ugięcia w prawo i w lewo na podstawie danych z tabeli nr. 1. Błędy zostały wyznaczone przy pomocy rozstępu z próby.

n=1

n=2

n=3

n=4

a1lśr'

a1pśr

a2lśr

a2pśr

a3lśr

a4pśr

186°12'

173°32'

193°00'

167°24'

200°4'

152°20'

Da

12'

22'

0'

44'

16'

20'

Następnie zostały policzone kąty ugięcia dla poszczególnych rzędów. Dla 1 i 2 rzędu ze wzoru:

Dla rzędów 3 i 4 ze względu pomiaru odchylenia tylko w jedną stronę zastosowany został wzór:

Błędy zostały obliczone metodą różniczki zupełnej. Otrzymano następujące wyniki :

a1 = 6°18' ± 17'

a2 = 12°48' ± 22'

a3 = 20°24' ± 10'

a4 = 27°20' ± 20'

Obliczenie stałej siatki dyfrakcyjnej:

Stałe siatki dyfrakcyjnej dla poszczególnych rzędów zostały wyliczone ze wzoru:

gdzie l = 589.3 nm - średnia długość fali żółtego dubletu sodu

Błędy zostały policzone z różniczki zupełnej:

gdzie Dan - błąd pomiaru kątów przeliczony na miarę łukową.

n=1

n=2

n=3

n=4

Następnie przy pomocy średniej ważonej została obliczona średnia wartość stałej siatki oraz jej błąd :

d=5.107*10-6 ± 3.167*10-8

Pomiar długości światła laserowego.

Na podstawie danych z tabeli nr. 2 oraz uprzednio wyliczonej stałej siatki wyliczamy długość światła światła laserowego ze wzoru:

gdzie : d -stała siatki dyfrakcyjnej

l - odległość siatki od ekranu

xn -odległości kolejnych prążków od prążka zerowego na ekranie

n - rząd prążka

Błędy zostały obliczone za pomocą różniczki zupełnej:

gdzie Dd -błąd względny stałej siatki

Dx = 5mm- błąd odczytu x

1 l,p) x=15.5 cm

2 l) x=32.5 cm

2 p) x=32.7 cm

3) x=49.5 cm

Następnie za pomocą średniej ważonej została wyliczona średnia długość światła oraz jej błąd :

lśr = 634.623 ± 6.16nm

Wyznaczenie szerokości szczeliny :

Z wyników pomiaru metodą fotoelektryczną zostały odczytane następujące położenia minimum (względem początku podziałki):

Rząd	x [mm] (lewo)	x [mm] (prawo)
0	6.8	15.684
1	2.684	20.350

Oraz położenie największego maksimum :

xmax = 10.850 mm

Z tych danych zostały obliczone odległości kolejnych minimów od osi układu :

1 l	0 l	0 p	1 p
8.167 mm	4.05 mm	4.834 mm	9.5 mm

Które zostały wstawione do wzoru jako x :

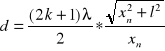
Błędy zostały policzone z różniczki zupełnej :

gdzie: Dl - błąd pomiaru l

Dx = 0.048 mm niepewność pomiarowa x

1 l) x = 4.05 mm

1 p) x = 4.834 mm

2 l) x = 8.167 mm

2 p) x = 9.5 mm

Za pomocą średniej ważonej obliczono średnią szerokość szczeliny oraz jej błąd :

dśr = 4.576*10-5 ± 3.489*10-7 m

Ze względu na duży rozstęp kolejnych obliczeń w stosunku do średniej (dużo większy niż wyliczony błąd), bardziej odpowiednią metodą obliczenia błędu dśr wydaje się metoda rozstępu z próby:

dśr = 0.046 ± 00013 mm

5.Podsumowanie.

Duży błąd w wyniku najprawdopodobniej jest spowodowany niezbyt precyzyjnym odczytaniem położenia maksimum w metodzie fotoelektrycznej spowodowane "postrzępieniem" miejscu odczytu.

---