Politechnika Warszawska Wydział Elektryczny Zakład Elektrotechniki Teoretycznej |
Laboratorium Elektrotechniki Teoretycznej |
||
Rok Semestr Gr. |
data godz. |
Ćwiczenie nr 10 Temat: Podstawowe czwórniki aktywne i ich zastosowanie. Część 2 |
|
Zespół nr :
|
Prowadzący:
|
Ocena:
4 pkt/4 |
|
Cel ćwiczenia:
Celem ćwiczenia było zapoznanie się z czwórnikami aktywnymi realizowanymi na wzmacniaczu operacyjnym: układem różniczkującym, całkującym i przesuwnikiem fazowym, ich charakterystykami amplitudowymi i fazowymi.
Podstawy teoretyczne:
Czwórniki aktywne zbudowane w oparciu o wzmacniacz operacyjny mogą realizować funkcje matematyczne np. sumowanie, mnożenie, logarytmowanie, różniczkowanie, całkowanie a także przesunięcia fazowe sygnałów.
Wzmacniacz operacyjny jest w istocie wzmacniaczem różnicowym (wzmacniacz liniowy z dwoma wejściami, w którym napięcie jest proporcjonalne do różnicy napięć wejściowych) o bardzo dużym wzmocnieniu (rzędu 104 ÷ 106) dla sygnału prądu stałego i zmiennego. Jego właściwości mogą być dość dowolnie kształtowane przez dobór odpowiedniego sprzężenia zwrotnego. Przez dobór odpowiednich kombinacje elementów wejściowych i sprzężenia zwrotnego można formować różne zależności między sygnałami wejściowymi i wyjściowymi. Umożliwia to tworzenie funkcji matematycznych oraz modelowanie zjawisk w układach fizycznych przy użyciu układów ze wzmacniaczami.
Stosunek napięcia wyjściowego do napięcia wejściowego nazywany jest transmitancją układu. Wyraża się ona wzorem
![]()
gdzie Z1(s) to impedancja wejściowa a Z2(s) to impedancja sprzężenia zwrotnego.
Zasada działania układu różniczkującego:
Schemat układu różniczkującego przedstawia rysunek poniżej.
Impedancje tego układu wynoszą Z1(s) = 1/(sC) a Z2(s) = R, więc transmitancja tego układu będzie wynosić
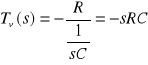
Mnożenie przez „s” odpowiada różniczkowaniu w funkcji czasu zatem odpowiedź układu w funkcji czasu będzie wyglądała następująco
![]()
przy założeniu ![]()
Wymuszenie sinusoidalne
Przedział < 0 ; T >
![]()
→ ![]()
Wymuszenie prostokątne
Przedział ( 0 ; T/2 )
![]()
→ ![]()
Przedział ( T/2 ; T )
![]()
→ ![]()
Rozpatrując tą funkcję w punktach charakterystycznych (t = 0, t = T/2, t = T) nie otrzymamy prostej tak jak zakładamy, gdyż w rzeczywistości w tych punktach następują skokowe zmiany napięcia zasilania. Dla tych punktów otrzymujemy następujące równania:
Dla t = 0
![]()
→ ![]()
Dla t = T/2
![]()
→ ![]()
Dla t = T
![]()
→ ![]()
Wymuszenie trójkątne
Przedział ( 0 ; T/4 )
![]()
→ ![]()
Przedział ( T/4 ; 3T/4 )
![]()
→ ![]()
Przedział ( 3T/4 ; T )
![]()
→ ![]()
Funkcja w punktach charakterystycznych (t = T/4, t = 3T/4) jest stała, a więc jej pochodna jest równa zero. Można stąd wywnioskować, że odpowiedź układu przechodząc z wartości „-a” do wartości „a” ma chwilową wartość zero.
Zasada działania układu całkującego:
Schemat układu całkującego przedstawia rysunek
Impedancje tego układu wynoszą Z1(s) = R a Z2(s) = 1/(sC), więc transmitancja tego układu będzie wynosić
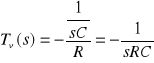
Dzielenie przez „s” odpowiada całkowaniu w funkcji czasu zatem odpowiedź układu w funkcji czasu będzie wyglądała następująco
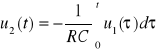
przy założeniu ![]()
Wymuszenie sinusoidalne
Przedział < 0 ; T >
![]()
→ ![]()
Wymuszenie prostokątne
Przedział < 0 ; T/2 )
![]()
→ ![]()
gdy ![]()
otrzymujemy ![]()
Przedział < T/2 ; T )
![]()
→ ![]()
gdy ![]()
otrzymujemy ![]()
Przedział ( T ; 3T/2 )
![]()
→ ![]()
gdy ![]()
otrzymujemy ![]()
Przedział < 3T/2 ; 2T )
![]()
→ ![]()
gdy ![]()
otrzymujemy ![]()
Wymuszenie trójkątne
Przedział < 0 ; T/4 )
![]()
→ ![]()
gdy ![]()
otrzymujemy ![]()
Przedział < T/4 ; 3T/4 )
![]()
→ ![]()
gdy ![]()
otrzymujemy 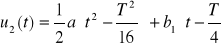
Przedział < 3T/4 ; T )
![]()
→ ![]()
gdy ![]()
otrzymujemy 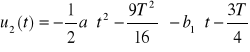
Wykonywanie ćwiczenia:
3.1 Badanie układu różniczkującego
Jak widać na schemacie wzmacniacz różniczkujący uzyskuje się przez zastąpienie rezystora na wejściu odwracającym wzmacniacza operacyjnego, kondensatorem C. Transmitancja takiego układu wyraża się wzorem TV= -sRC
Stąd wiemy, że napięcie na wyjściu będzie iloczynem transmitancji i napięcia wejściowego: Uwy(s)= -sRCUwe(s). A więc wiedząc, że wejście odwracające wzmacniacza operacyjnego jest punktem masy pozornej, składowa zmienna napięcia powoduje przepływ prądu I=C(dUwe/dt), który wytwarza na wyjściu napięcie Uwy= -RC(dUwe/dt). Widać stąd, że napięcie na wyjściu układu jest pochodną napięcia wejściowego ze współczynnikiem proporcjonalności -RC.
Dla wymuszenia sinusoidalnego Uwe= Umsin(ωt) napięcie wyjściowe przyjmuje postać: Uwy(t)= -RCUmcos(ωt). Zatem dla rosnącej częstotliwości f napięcie wejściowe rośnie.
Naszym zadaniem badając ten układ było zdjąć dwie charakterystyki:
Uwy=f(f) (Uwe=0,707V)
Uwy=f(Uwe): (f=500Hz)
Pulsacji ω
Rezystancji Rφ
Pojemności C.
Układ całkujący (przebieg sygnału wejściowego)
Układ różniczkujący (przebieg sygnału wejściowego)
Przesuwnik fazowy
Dla układu różniczkującego:
Dla układu całkującego:
Dla przesuwnika fazowego:
f [Hz] |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1k |
1,1k |
1,2k |
1,3k |
1,4k |
1,5k |
2k |
Uwy [V] |
0,924 |
1,37 |
1,83 |
2,27 |
2,72 |
3,17 |
3,61 |
4,04 |
4,46 |
4,89 |
5,31 |
5,71 |
6,11 |
6,52 |
8,41 |
Uwe[V] |
0,377 |
0,58 |
0,72 |
0,86 |
1 |
1,28 |
1,69 |
1,97 |
2,53 |
Uwy[V] |
1,13 |
1,81 |
2,26 |
2,72 |
3,18 |
4,06 |
5,44 |
6,33 |
8,09 |
3.2 Układ całkujący (integrator)
Integrator otrzymujemy włączając w obwód sprzężenia zwrotnego kondensator C. Transmitancja takiego układu wyraża się wzorem TV= -1/sRC, więc napięcie wyjściowe można przedstawić w postaci Uwy(s)= -1/sRC Uwe(s). Prąd wejściowy o wartości Uwe/R przepływa przez kondensator C. ponieważ wejście odwracające wzmacniacza jest punktem masy pozornej, napięcie wyjściowe spełnia następującą zależność: Uwe/R = -C(dUwy/dt) lub po przekształceniu:
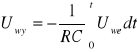
Zatem można zauważyć że napięcie wyjściowe jest całką napięcia wejściowego.
Dla wymuszenia sinusoidalnego Uwe=Umsin(ωt) napięcie wyjściowe przyjmuje postać: Uwy(t)=Umcos(ωt)/RCω. Zatem dla rosnącej częstotliwości f napięcie na wyjściu maleje.
Podobnie jak poprzednio musieliśmy zdjąć dwie charakterystyki:
1. Uwy=f(f): (Uwe=0,707V)
f [Hz] |
100 |
500 |
1k |
1,5k |
2k |
Uwy[V] |
0,575 |
0,116 |
0,06 |
0,04 |
0,03 |
2. Uwy=f(Uwe): (f=500Hz)
Uwe[V] |
0,352 |
0,493 |
0,704 |
1,06 |
1,41 |
1,77 |
2,12 |
2,46 |
Uwy[mV] |
59 |
81 |
115 |
173 |
229 |
287 |
346 |
402 |
3.3 Badanie przesuwnika fazowego:
W tej części ćwiczenia badaliśmy układ przesuwnika fazowego. Układ ten jest opisany następującymi równaniami:
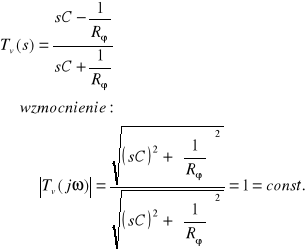
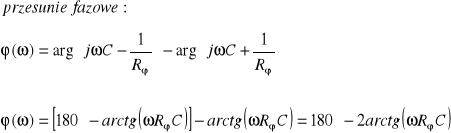
Wynika z tego, że układ realizuje przesunięcie fazowe w przedziale 0-180º zależnie od trzech parametrów:
Wszystkie parametry rosnąć powodują przesunięcie fazowe począwszy od 180º w kierunku 0º.
Wzmocnienie natomiast nie zależy od tych parametrów. Przy doborze rezystorów pętli sprzężenia zwrotnego R1=R2=R wzmocnienie układu jest równe 1 (nie uwzględniając przesunięcia fazowego, które już zostało wyszczególnione wcześniej).
Oto tabele pomiarowe:
|
|
|
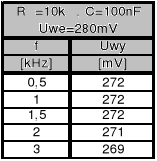
Z pierwszej tabeli wynika, że wzmocnienie nie zależy od częstotliwości co potwierdza teoretyczne równania opisujące działanie układu co do wzmocnienia. Należy jednak pamiętać, że wzmacniacz ma duże ale jednak skończone wzmocnienie, które maleje wraz ze wzrostem częstotliwości. Powodować to może, że wraz ze wzrostem częstotliwości może spadać amplituda sygnału wyjściowego co też widać pod koniec tabeli przy częstotliwości 3kHz.
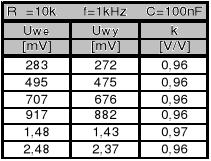
Z drugiej tabeli wynika również, że wzmocnienie nie zależy od napięcia wejściowego. Jest to oczywiste gdyż jak wynika z równań napięcie wyjściowe jest związane z wejściowym przez współczynnik proporcjonalności k - wzmocnieniem napięciowym, który jest stałe. Ta zależność jest zachowana do momentu nasycenia się wzmacniacza operacyjnego. Na podstawie tabeli można powiedzieć, że wzmocnienie układu jest równe w przybliżeniu 1.
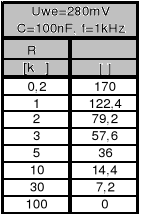
Z trzeciej tabeli wynika, że układ wraz ze zmianą parametru Rφ powoduje przesunięcie fazowe sygnału wyjściowego względem sygnału wejściowego. Coprawda podstawiając wartości do wzorów powyżej nie uzyskamy identycznych wyników lecz trzeba pamiętać, że jest to układ rzeczywisty i równania teoretyczne nie do końca oddają wszystkie zjawiska dziejące się w obwodzie. Jednakże tendencja spadku przesunięcia fazowego jest zachowana wraz ze wzrostem Rφ co potwierdza najważniejszą i pożądaną właściwość tego układu.
4. Wnioski:
W tym ćwiczeni badaliśmy układy czwórników aktywnych:
Wyniki pomiarów wykazały, że zarówno układ całkujący jak i różniczkujący wykonują prawidłowe przetwarzanie sygnały wejściowego (uwzględniając to, że sygnały wejściowe były podawane na wejścia odwracające fazę wzmacniacza operacyjnego). Widać również, że wzmocnienie tych układów jest zależne od częstotliwości. Wynika to ze zmienności reaktancji kondensatora przy zmianach pulsacji.
Charakteryzuje się on liniową zależnością wzmocnienia od częstotliwości. Natomiast samo zjawisko różniczkowania sygnału wejściowego jest uwidocznione na wykresach i jest realizowane prawidłowo. Z przebiegu trójkątnego podanego na wejście układ dał odpowiedź na wyjściu falę prostokątną. Należy jednak dopowiedzieć, że w przypadku sygnału wejściowego w postaci fali prostokątnej odpowiedź układu (z matematycznego punktu widzenia) powinna być w postaci impulsu Dirac'a (o nieskończonej amplitudzie). Jednakże należy pamiętać, że czas narastania zbocza fali prostokątnej nie jest zerowy, jak również, że wzmacniacz jak i obwód jest rzeczywisty i maksymalne napięcie jakie może dać wzmacniacz jest ograniczone napięciem zasilania (±15V).
Charakteryzuje się on odwrotną proporcjonalnością wzmocnienia od częstotliwości. Wynika to z tego, że kondensator jest umieszczony w pętli sprzężenia zwrotnego. W związku z tym napięcie wyjściowe jest proporcjonalne do napięcia na nim a ono z kolei jest proporcjonalne do jego reaktancji która jest odwrotnie proporcjonalna do częstotliwości. Jeśli natomiast chodzi o kształt charakterystyk wychodzących z układu przy pobudzaniu go odpowiednimi sygnałami na wejściu to możemy powiedzieć, że układ całkuje zgodnie z zależnościami matematycznymi. Z fali prostokątnej na wejściu powstaje na wyjściu przebieg trójkątny natomiast z przebiegu trójkątnego powstaje sinusoida.
Przesuwnik fazowy realizował przesunięcie fazowe przebiegu sinusoidalnego podawanego na wejście układu. Zgodnie w równaniami opisującymi jego właściwości czwórnik realizował przesunięcie fazowe w funkcji rezystancji Rφ wg wzoru ![]()
. Charakteryzował się również stałym wzmocnieniem k=1 niezależnym od Rφ, C czy częstotliwości.
Wykonane pomiary wykazały poprawność działania wszystkich badanych układów.
10
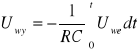
Wyszukiwarka
Podobne podstrony:
Czwórniki aktywne (część 1), POLITECHNIKA WARSZAWSKA
Cześć, Politechnika Warszawska Wydział Transportu, Semestr VI, Technoka Pomiarowa Laboratoria, różno
Projektowanie sekcji bikwadratowej filtrów aktywnych, POLITECHNIKA WARSZAWSKA
A2-3, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynieria kom
slajdy TIOB W27 B montaz obnizone temperatury, Przodki IL PW Inżynieria Lądowa budownictwo Politechn
Politechnika Warszawska
test z wydymałki, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Wy
zagrożenia bhp przy robotach, Politechnika Warszawska, Organizacja Placu Budowy, Wykład
OPIS DROGI, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynier
EPS semestr VI, Politechnika Warszawska Wydział Transportu, Semestr VII, Eksploatacja Pojazdów Samoc
Irek, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynieria kom
spr3asia, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Wytrzymało
Politechnika Warszawska
Politechnika Warszawska
więcej podobnych podstron