Politechnika Warszawska Wydział Elektryczny Zakład Elektrotechniki Teoretycznej		Laboratorium Elektrotechniki Teoretycznej
Rok Semestr Gr.	data godz.	Ćwiczenie nr 11 Temat: Projektowanie sekcji bikwadratowej filtrów aktywnych
Zespół nr :		Prowadzący:	Ocena: 3 pkt/4

1. Cel ćwiczenia:

Celem ćwiczenia było zapoznanie się z podstawowymi filtrami elektrycznymi o charakterystyce dolno-, środkowo- i górnoprzepustowej, charakterystykami częstotliwościowymi filtrów, projektowaniem filtrów w strukturze KHN o zadanych parametrach częstotliwościowych oraz pomiarem dobroci i częstotliwości krytycznej.

2. Podstawy teoretyczne:

Filtr elektryczny jest to czwórnik , który w pewnym przedziale częstotliwości przepuszcza sygnały wejściowe zaś w innym tłumi je. Filtry są opisywane w dziedzinie przekształcenia Laplace'a przez transmitancje operatorowe, najczęściej transmitancje napięciowe.

W ćwiczeniu ograniczymy rozważania do filtrów dolno-, górno- i środkowoprzepustowych drugiego rzędu, tj. o transmitancji napięciowej wyrażonej ilorazem funkcji drugiego stopnia zwanej sekcją bikwadratową:

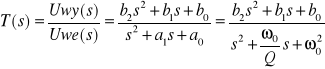
gdzie:

a_i, b_i - współczynniki rzeczywiste

ω₀ - pulsacja krytyczna

Q - dobroć filtru

W zależności od istnienia współczynników b₀, b₁, b₂ otrzymuje się transmitancje filtrów:

a) istnieje tylko
- filtr dolnoprzepustowy

b) istnieje tylko
- filtr środkowoprzepustowy

c) istnieje tylko
- filtr górnoprzepustowy

Jedną ze struktur pozwalających na zrealizowanie wszystkich trzech omówionych rodzajów filtrów jest konfiguracja Kerwina-Heulsmana-Newcomba (zwana strukturą KHN). Poniższy schemat przedstawia filtr KHN z wejściem odwracającym.

Wyjścia poszczególnych wzmacniaczy reprezentują odpowiednie wyjścia filtru dolno-, środkowo- i górnoprzepustowego.

3. Wykonanie ćwiczenia

Naszym zadaniem było zaprojektowanie filtru środkowoprzepustowego o następujących parametrach

A_SP = 3, f₀ = 750 Hz, Q = 5

Znając wartości R = 20kΩ, C = 11nF i R_G = 10kΩ obliczyliśmy wartości R_f i R_Q korzystając z wzorów:

1. Filtr dolnoprzepustowy

Transmitancja tego filtru wyrażona jest następująco:

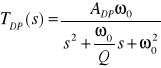
gdzie A_DP oznacza wzmocnienie filtru w paśmie przepustowym. Podstawiając s=jω otrzymuje się charakterystyki częstotliwościowe

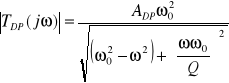
natomiast charakterystyka fazowa tego filtru wyraża się zależnością:

Dla dobroci
charakterystyka amplitudowa jest niemonotoniczna i osiąga maksimum dla częstotliwości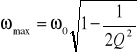
. Wynika stąd, że ω_max (jeśli występuje) jest różne od częstotliwości krytycznej ω₀. Chcąc wyznaczyć ω₀ należy znać lub wyznaczyć dobroć filtru Q. Można to zrobić z zależności

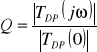
Zależność ta jest słuszna niezależnie od wartości Q. Dla
przy pulsacji ω₀ wzmocnienie maleje o
razy, czyli o 3 dB. Pulsację tę interpretuje się jako

3-decybelową pulsację graniczną.

Wyniki naszych pomiarów odczytane z otrzymanej charakterystyki prezentuje poniższa tabela:

Lp.	f	Uwe	Uwy	k
		[Hz]	[V]	[V]	[V/V]
1	100	2,26	4,24	1,88
2	200	2,26	4,52	2,00
3	300	2,26	4,95	2,19
4	400	2,26	5,23	2,31
5	500	2,26	5,94	2,63
6	600	2,26	6,79	3,00
7	700	2,26	7,35	3,25
8	800	2,26	6,36	2,81
9	900	2,26	4,95	2,19
10	1000	2,26	3,74	1,65
11	1100	2,26	2,83	1,25

Największe wzmocnienie (A_DP = 3,25) filtr osiągnął dla częstotliwości 700 Hz. Zakres przenoszonych częstotliwości wyznaczymy poprzez odczytanie z wykresu punktu odpowiadającemu wzmocnieniu
. Jest to częstotliwość

f₀ = 880 Hz. Dobroć naszego filtru wynosiła
, co jest wartością większą od
, a więc charakterystyka amplitudowa jest niemonotoniczna. Jeżeli przyjmiemy częstotliwość f₀ = 880 Hz to możemy wyznaczyć częstotliwość f_max tego filtru ze wzoru:

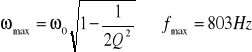
Widać tu że wielkości wyliczone i odczytane z wykresu odbiegają od siebie. Jest po prawdopodobnie skutkiem błędów pomiarowych i trudności w dokładnym odczytaniu wartości częstotliwości z wykresów.

Transmitancja otrzymanego filtru dolnoprzepustowego wyraża się wzorem:

f₀ = 803 Hz

Q = 1,73

2. Filtr środokowoprzepustowy:

Transmitancja tego filtru wyrażona jest następująco:

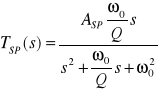
gdzie A_SP oznacza wzmocnienie filtru w paśmie przepustowym. Podstawiając s=jω otrzymuje się charakterystyki częstotliwościowe:

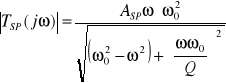
natomiast charakterystyka fazowa tego filtru wyraża się zależnością:

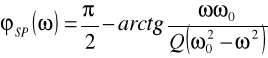
Pulsacja środkowa ω₀ odpowiada maksimum charakterystyki amplitudowej. Natomiast dobroć Q określa stosunek pulsacji środkowej ω₀ (rezonansowej) do 3-decybelowego pasma przenoszenia Δω₀:

Wyniki naszych pomiarów odczytane z otrzymanej charakterystyki prezentuje poniższa tabela:

Lp.	f	Uwe	Uwy	k
		[Hz]	[V]	[V]	[V/V]
1	100	2,26	0,85	0,38
2	200	2,26	1,41	0,62
3	300	2,26	2,12	0,94
4	400	2,26	2,97	1,31
5	500	2,26	4,03	1,78
6	600	2,26	5,65	2,5
7	700	2,26	6,72	2,97
8	800	2,26	6,64	2,94
9	900	2,26	5,51	2,44
10	1000	2,26	4,8	2,12
11	1100	2,26	4,3	1,93

Największe wzmocnienie (A_SP = 2,97) filtr osiągnął dla częstotliwości

700 Hz stąd ω₀= 4398,1. Zakres przenoszonych częstotliwości wyznaczymy poprzez odczytanie z wykresu punktów odpowiadających wzmocnieniu
równy jest 1000Hz-550Hz=450Hz=Δf stąd Δω₀= 2827,35. Dobroć naszego filtru wynosiła
.

Widać tu że wielkości wyliczone i odczytane z wykresu odbiegają od siebie. Jest po prawdopodobnie skutkiem błędów pomiarowych i trudności w dokładnym odczytaniu wartości częstotliwości z wykresów.

Transmitancja otrzymanego filtru dolnoprzepustowego wyraża się wzorem:

f₀ = 700 Hz

Q = 1,55

3. Filtr górnoprzepustowy:

Transmitancja tego filtru wyrażona jest następująco:

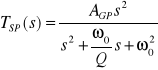
gdzie A_GP oznacza wzmocnienie filtru w paśmie przepustowym (liczone dla s=j
). Podstawiając s=jω otrzymuje się charakterystyki częstotliwościowe:

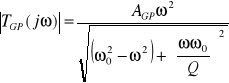
natomiast charakterystyka fazowa tego filtru wyraża się zależnością:

Dla dobroci
charakterystyka amplitudowa osiąga maksimum dla częstotliwości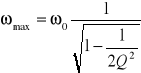
. Wynika stąd, że ω_max (jeśli występuje) jest różne od częstotliwości krytycznej ω₀. Chcąc wyznaczyć ω₀ należy znać lub wyznaczyć dobroć filtru Q. Można to zrobić z zależności

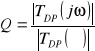
Wyniki naszych pomiarów odczytane z otrzymanej charakterystyki prezentuje poniższa tabela:

Lp.	f	Uwe	Uwy	K
		[Hz]	[V]	[V]	[V/V]
1	100	2,26	0,28	0,12
2	200	2,26	0,41	0,19
3	300	2,26	0,98	0,43
4	400	2,26	1,69	0,75
5	500	2,26	2,83	1,25
6	600	2,26	4,52	2,00
7	700	2,26	6,36	2,81
8	800	2,26	7,07	3,13
9	900	2,26	6,92	3,06
10	1000	2,26	6,22	2,75
11	1100	2,26	5,94	2,63

Największe wzmocnienie (A_GPmax =3,13) filtr osiągnął dla częstotliwości

800 Hz stąd ω_max= 5026,5. Zakres przenoszonych częstotliwości wyznaczymy poprzez odczytanie z wykresu punktu odpowiadającemu wzmocnieniu
równy jest 650Hz=fo stąd ω₀=4084. Dobroć naszego filtru wynosiła
.

Transmitancja otrzymanego filtru dolnoprzepustowego wyraża się wzorem:

f₀ = 650 Hz

Q = 1,19

3.4 Obliczenie odpowiedzi układu filtru środkowoprzepustowego na skok jednostkowy:

Dodatkowo postanowiliśmy wyliczyć odpowiedź układu na skok jednostkowy. Obliczenia są następujące:

4. WNIOSKI:

Wykonane ćwiczenie pozwoliło nam na zbadanie właściwości filtrów dolnoprzepustowego, środkowoprzepustorego i górnoprzepustowego. Na otrzymanych wykresach obserwujemy charakterystyki amplitudowe badanych filtrów. Widać ich częstotliwości charakterystyczne oraz zachowanie się wzmocnienia w funkcji częstotliwości.

Projektowany przez nas filtr posiadał dużą dobroć i przez to charakterystyki amplitudowe mają przebiegi niemonotoniczne. Widać również typowe kształty charakterystyk wzmocnienia od częstotliwości które świadczą o charakterze filtru.

Na ekranie oscyloskopu zaobserwowaliśmy również odpowiedź układu na skok jednostkowy (ustawiliśmy w tym celu na generatorze przebieg prostokątny). Odpowiedź układu (na zbocze przebiegu prostokątnego) charakteryzowała się drganiami sinusoidalnymi gasnącymi wykładniczo. Przebieg ten po wygaśnięciu stawał się linią prostą.

Wyliczone wielkości parametrów filtrów różnią się od przyjętych podczas projektowania filtru. Jest to wynikiem rzeczywistych warunków pracy układów.

Jednakże widac że filtry kształtują sygnał wejściowy w sposób prawidłowy co daje nam bardo dobre i uniwersalne narzędzie do przy projektowaniu filtrów o charakterystykach i parametrach jakich potrzebujemy.

8

---