Zadanie 1

Zbadano przebiegi 200 opon samochodowych pewnego typu wycofanych z eksploatacji i otrzymano wyniki

Przebiegi opon (tys. km)	25-30	30-35	35-40	40-45	45-50	50-55
Liczba opon	15	30	65	55	25	10

Na poziomie istotności 0,05 zweryfikować hipotezę, że rozkład przebiegu opon jest normalny.

Obliczenia pomocnicze

xio - xi1		ni
25-30	27,5	15	412,5	2115,23
30-35	32,5	30	975,0	1417,97
35-40	37,5	65	2437,5	228,52
40-45	42,5	55	2337,5	537,11
45-50	47,5	25	1187,5	1650,39
50-55	52,5	10	525,0	1722,66
suma		200	7875,0	7671,88

średnia z próby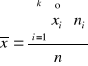

wariancja z próby

odchylenie standardowe z próby
≈ 6,1935

xio - xi1	ni	nski		xi1
poniżej 30	15	15	0,0750	30	-1,51	0,0655	0,0095
30-35	30	45	0,2250	35	-0,71	0,2389	0,0139
35-40	65	110	0,5500	40	0,10	0,5398	0,0102
40-45	55	165	0,8250	45	0,91	0,8186	0,0064
45-50	25	190	0,9500	50	1,72	0,9573	0,0073
50 i więcej	10	200	1,0000	x	x	1	0,0000
suma	200

Test zgodności λ Kołmogorowa

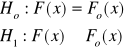
F(x) dystrybuanta badanej cechy w populacji

F_o(x) dystrybuanta rozkładu normalnego

= 0,0139

dystrybuanta empiryczna policzona dla górnej granicy i-tego przedziału, i = 1, 2, ..., k

dystrybuanta rozkładu normalnego odczytana z tablic dla standaryzowanej górnej granicy i-tego przedziału

Statystyka testowa ma postać:
=

Obszar krytyczny jest prawostronny - wartość krytyczna

Z tablic rozkładu granicznego λ-Kołmogorowa odczytujemy wartość dystrybuanty

= 0,95

F(1,36) = 0,950512 ⇒
= 1,36

Wartość statystyki z próby λ = 0,1966 nie znalazła się w obszarze krytycznym
, na poziomie istotności 0,05 nie ma więc podstaw do odrzucenia hipotezy zerowej mówiącej, że rozkład przebiegu opon jest normalny.

Zadanie 2

Wzrost (w cm) wylosowanych studentów był następujący:

173, 180, 182, 170, 175, 180, 165, 195, 187, 177

1. Na poziomie istotności 0,05 zweryfikuj hipotezę, że dobór studentów do próby był losowy.

2. Na poziomie istotności 0,05 zweryfikuj hipotezę, że próba pochodziła z rozkładu normalnego.

a) Test losowości próby

Test serii Stevensa

H_o: dobór jednostek do próby jest losowy

H₁: dobór jednostek do próby nie jest losowy

1) Wyznaczamy medianę

Porządkujemy dane rosnąco: 165, 170, 173, 175, 177, | 180, 180, 182, 187, 195

2. Tworzymy ciąg składający się z symboli A i B dla wyników z próby w kolejności pojawiania się

symbol A zastępuje wartości x_i < Me

symbol B zastępuje wartości x_i > Me

(wartości x_i = Me pomijamy)

A B B A A B A B B A

3. Liczba serii k = 7 jest wartością statystyki z próby

4. Obszar krytyczny jest dwustronny - wartości krytyczne k₁ i k₂ odczytujemy z tablic rozkładu liczby serii K w zależności od poziomu istotności α oraz n_A - liczby symboli A i n_B - liczby symboli B

= k(0,025; 5; 5) = 2

= k(0,975; 5; 5) = 9

5) Podjęcie decyzji:
⇒ nie ma podstaw do odrzucenia H_o

Wartość statystyki z próby nie znalazła się w obszarze krytycznym, na poziomie istotności 0,05 nie ma więc podstaw do odrzucenia hipotezy zerowej mówiącej, że dobór studentów do próby był losowy.

b) Test zgodności z rozkładem normalnym

Test zgodności Kołmogorowa-Smirnowa

Założenia: próba mała (n < 100), wyniki z próby dane w szeregu szczegółowym

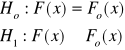
F(x) dystrybuanta badanej cechy w populacji

F_o(x) dystrybuanta rozkładu normalnego

Obliczenia pomocnicze dla danych uporządkowanych rosnąco

i	xi
1	165	179,56	-1,65	0,0495	0,1	0,0505	0	0,0495
2	170	70,56	-1,03	0,1515	0,2	0,0485	0,1	0,0515
3	173	29,16	-0,66	0,2546	0,3	0,0454	0,2	0,0546
4	175	11,56	-0,42	0,3372	0,4	0,0628	0,3	0,0372
5	177	1,96	-0,17	0,4325	0,5	0,0675	0,4	0,0325
6	180	2,56	0,20	0,5793	0,6	0,0207	0,5	0,0793
7	180	2,56	0,20	0,5793	0,7	0,1207	0,6	-0,0207
8	182	12,96	0,44	0,6700	0,8	0,1300	0,7	-0,0300
9	187	73,96	1,06	0,8554	0,9	0,0446	0,8	0,0554
10	195	275,56	2,04	0,9793	1	0,0207	0,9	0,0793
suma	1784	660,4

średnia z próby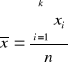

wariancja z próby

odchylenie standardowe z próby
≈ 8,1265

= 0,1300

= 0,0793

Statystyka testowa ma postać:
= max(0,1300; 0,0793) = 0,1300

Obszar krytyczny jest prawostronny - wartość krytyczną
odczytuje się z tablic wartości krytycznych rozkładu statystyki D przy nieznanych parametrach μ i σ dla α = 0,05 i n = 10
= 0,258

Wartość statystyki z próby D_n = 0,13 nie znalazła się w obszarze krytycznym
, na poziomie istotności 0,05 nie ma więc podstaw do odrzucenia hipotezy zerowej mówiącej, że rozkład wzrostu studentów jest normalny.

Wskazówka

Porównaj przykłady z podręcznika Balicki A., Makać W. „Metody wnioskowania statystycznego”, Wydawnictwo UG, Gdańsk 2002

2

---