Opole, dn. 21 kwietnia 2004

Laboratorium Algorytmów i Struktur Danych

Temat:

Analiza algorytmu wyszukiwania miejsc zerowych funkcji

Autor: Dawid Najgiebauer

Informatyka, sem. II, grupa lab. 11

Prowadzący: dr inż. Jan Sadecki

1. Temat

Zaprojektować i zbadać algorytmy wyszukujące miejsca zerowe funkcji, zadanej wzorem:

W analizie wykorzystać algorytm wyszukiwania:

• naturalnego,

• przez bisekcję,

• metodą siecznych

• metodą stycznych (Newtona).

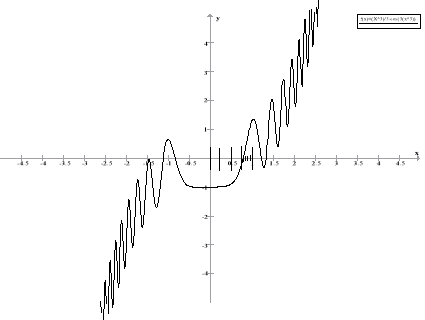
Wykres zadanej funkcji przedstawia poniższy rysunek:

Rysunek 1. Wykres badanej funkcji

2. Analiza, projektowanie

Jak widać z rysunku 1, funkcja posiada 5 miejsc zerowych. Podczas badania algorytmów, będą one wyszukiwać miejsca zerowego w przedziale <0,1>. Wyjątkiem będzie algorytm wyszukiwania metodą siecznych, gdyż w tym przypadku spełnione muszą być dodatkowe założenia (por. p. 2.4).

1. Wyszukiwanie naturalne (liniowe)

Metoda ta opiera się na podziale badanego odcinka na określoną ilość części po osi X. Następnie badane jest, czy w miejscu podziału występuje miejsce zerowe. Jeśli nie, to wyszukiwany jest podprzedział powstały po podziale, w którym następuje zmiana znaku funkcji. Dany podprzedział jest następnie ponownie dzielony wg powyższej metody. Operacje te są przeprowadzane aż do momentu znalezienia miejsca zerowego.

2. Wyszukiwanie przez bisekcję

Metoda ta jest podobna do poprzedniej. Jednak badany przedział dzielony jest wyłącznie na pół. Dzięki temu można znacząco uprościć kod.

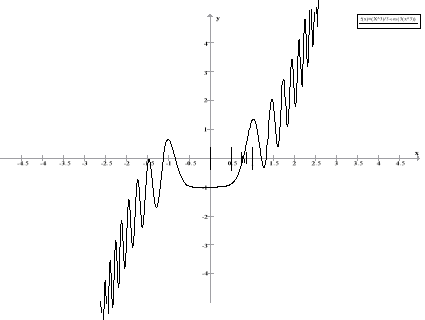
3. Wyszukiwanie metodą siecznych

Wyszukiwanie metodą siecznych opiera się na rysowaniu siecznej przechodzącej przez końce badanego przedziału, a następnie tworzenie nowego przedziału, gdzie jednym z końców jest wartość, w której następuje przecięcie siecznej z osią OX.

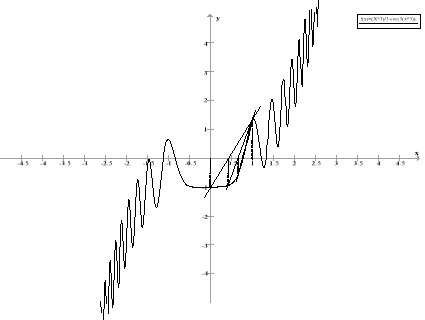
4. Wyszukiwanie metodą stycznych (Newtona)

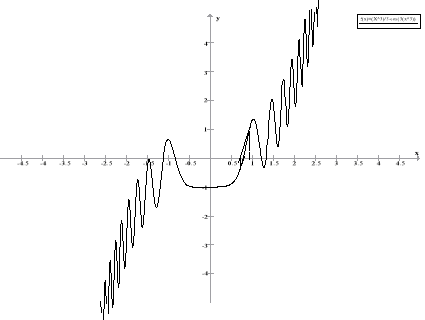
Metoda ta polega na szukaniu pierwiastka f(x) przez przybliżanie się do niego w kolejnych krokach, podobnie jak w metodzie poprzedniej. Lecz tutaj kolejną wartość wyznacza miejsce przecięcia się stycznej do wykresu w danym punkcie.

Problemem w tej metodzie jest określenie punktu startowego. Punkt ten musi być dostatecznie blisko pierwiastka funkcji. W tym celu trzeba trzymać się dwóch zasad:

1. Trzeba znaleźć taki przedział <a,b> zwierający x₀, aby istniał w nim dokładnie jeden pierwiastek. W tym celu dobiera się a i b tak, aby znaki f(a) i f(b) były różne oraz aby f'(x) w tym przedziale nie zmieniała znaku. Jeśli f(a) i f(b) mają różne znaki, przedział zawiera co najmniej jeden pierwiastek. Jeśli znak f'(x) w przedziale <a,b> się nie zmienia, przedział ten zawiera tylko jeden pierwiastek, gdyż funkcja jest monotoniczna.

2. Wybieramy x₀=a lub x₀=b tak, aby f(x₀) miała taki sam znak, jak f'(x) w przedziale <a,b>. Chcemy, aby w wybranym przedziale także druga pochodna nie zmieniała znaku. Jeśli f'(x) nie zmienia znaku oraz x₀ wybrano tak, aby f(x₀) miała taki sam znak, jak f'(x), kolejne kroki metody Newtona będą zbliżały do pierwiastka zawartego w odcinku <a,b>.

3. Specyfikacja wewnętrzna, implementacje algorytmów

1. Funkcje pomocnicze

#define sign(x) (int)((x>=0)?1:-1)

Funkcja zwraca znak liczby: -1 - dla wartosci ujemnej 1 - dla wartości 0 lub dodatniej

double f(double x)

Funkcja zwraca wartość badanej funkcji w punkcie. Parametry: x - badany punkt x0 funkcji.

double df(double x)

Funkcja zwraca wartość pochodnej badanej funkcji w punkcie. Parametry: x - badany punkt x0 funkcji.

char zero(double x)

Funkcja sprawdza, czy zadana wartość jest zerem (lub bliska zeru; |x|<ε). Parametry: x - badana wartość. Zwracane wartości: 0 - wartość nie jest zerem ani jemu bliska. 1 - wartość jest zerem lub bliska zeru.

2. Implementacja algorytmu wyszukiwania metodą naturalną

double zer_natur(double a, double b)

{

double x=a;

char znak;

double skok=(b-a)/10.0;

wywolan++;

if (sign(f(a))==sign(f(b))) return 0;

znak=sign(f(x));

for(x=a+skok;x<=b;x+=skok)

{

if (zero(x)) return x;

else

if (znak!=sign(f(x))) return zer_natur(x-skok,x);

}

return 0;

}

3. Implementacja algorytmu wyszukiwania metodą bisekcji

double zer_bis(double a, double b)

{

wywolan++;

if (zero((a+b)/2.0)) return (a+b)/2.0;

if (sign(f(a))!=sign(f((a+b)/2.0))) return zer_bis(a,(a+b)/2.0);

else return zer_bis((a+b)/2.0,b);

}

4. Implementacja algorytmu wyszukiwania metodą bisekcji

double zer_bis(double a, double b)

{

wywolan++;

if (zero((a+b)/2.0)) return (a+b)/2.0;

if (sign(f(a))!=sign(f((a+b)/2.0))) return zer_bis(a,(a+b)/2.0);

else return zer_bis((a+b)/2.0,b);

}

5. Implementacja algorytmu wyszukiwania metodą siecznych

double zer_siecz(double a, double b)

{

double A,B,x;

wywolan++;

A=(f(b)-f(a))/(b-a);

B=f(a)-A*a;

x=-B/A;

if (zero(x)) return x;

if (sign(f(a))!=sign(f(x))) return zer_siecz(a,x);

else return zer_siecz(x,b);

}

6. Implementacja algorytmu wyszukiwania metodą stycznych

double zer_stycz(double a, double b)

{

double A,B,x,z;

wywolan++;

if (sign(f(a))==sign(df(a))) x=a; else x=b;

A=df(x);

if (zero(A)) return 0;

B=f(x)-A*x;

z=-B/A;

if ((z<a) || (z>b)) return 0;

if (zero(z)) return z;

if (sign(f(a))!=sign(f(z))) return zer_stycz(a,z);

else return zer_stycz(z,b);

}

4. Badanie i wnioski z testowania i uruchamiania

Badanie zostało przeprowadzone przy zadanej dokładności wynoszącej ε=10^-6. Wyniki działania funkcji przedstawiono w poniższej tabelce:

Tabela 1. Wyniki działania algorytmów

Metoda	Wynik	Liczba wywołań
Naturalna	0,778073	7
Bisekcji	0,778073	21
Siecznych	0,778073	6
Stycznych (Newtona)	0,778073	3

Z przeprowadzonych badań wynikają następujące wnioski:

1. Wszystkie metody zwracają poprawny identyczny wynik.

2. Najwięcej wywołań pochłonęła metoda bisekcji; najmniej - stycznych.

3. Metoda stycznych nakłada bardzo duże wymagania wobec doboru badanego przedziału oraz stawia warunki bardzo trudne do optymalnego określenia punktu startowego. W związku z tym może, w zależności od trafności doboru przedziału, dawać wyniki bardzo szybko, jak i - przy niewłaściwej analizie funkcji - nie zwrócić żadnego wyniku, co nie ma prawa zdarzyć się w pozostałych metodach.

4. Optymalność wszystkich metod uzależniona jest od kształtu badanej funkcji.

8 Dawid Najgiebauer

Badanie i wnioski z testowania i uruchamiania 9

Temat 3

---